题目内容
已知函数f(x)=
g(x)=x2+2x,则方程f[g(x)]=a(a>2)的根的个数不可能为( )
|
| A、3 | B、4 | C、5 | D、6 |
考点:分段函数的应用,根的存在性及根的个数判断
专题:函数的性质及应用
分析:利用换元法将方程进行分解,作出对应的图象,利用数形结合即可得到结论.
解答:
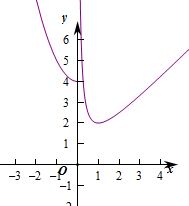 解:设t=g(x),则方程等价为f(t)=a,a>2,
解:设t=g(x),则方程等价为f(t)=a,a>2,
作出f(x)的图象如图:
∵a>2,
∴当a≥4时,f(t)=a有三个解,满足t≤0或者0<t<1或t>1.
当2<a<4时,f(t)=a有两个解,满足0<t<1或t>1.
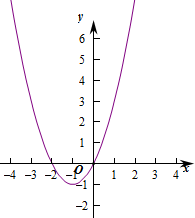
对应g(x)的图象为:
则当t>1时,方程t=g(x),有两个根,
当0<t<1时,方程t=g(x),有两个根,
当t≤0时,方程t=g(x),可能有两个根,可能有一个,可能没有,
即方程方程f[g(x)]=a(a>2)至少有4个根,
故方程f[g(x)]=a(a>2)的根的个数不可能为3,
故选:A
 解:设t=g(x),则方程等价为f(t)=a,a>2,
解:设t=g(x),则方程等价为f(t)=a,a>2,作出f(x)的图象如图:
∵a>2,
∴当a≥4时,f(t)=a有三个解,满足t≤0或者0<t<1或t>1.
当2<a<4时,f(t)=a有两个解,满足0<t<1或t>1.
对应g(x)的图象为:
则当t>1时,方程t=g(x),有两个根,
当0<t<1时,方程t=g(x),有两个根,
当t≤0时,方程t=g(x),可能有两个根,可能有一个,可能没有,
即方程方程f[g(x)]=a(a>2)至少有4个根,
故方程f[g(x)]=a(a>2)的根的个数不可能为3,
故选:A

点评:本题主要考查方程根的个数的判断,利用换元法以及数形结合是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
若x1,x2是方程2x2-4x+1=0的两个根,则
+
的值为( )
| x1 |
| x2 |
| x2 |
| x1 |
| A、6 | ||
| B、4 | ||
| C、3 | ||
D、
|
从装有2个白球和2个蓝球的口袋中任取2个球,那么对立的两个事件是( )
| A、“恰有一个白球”与“恰有两个白球” |
| B、“至少有一个白球”与“至少有-个蓝球” |
| C、“至少有-个白球”与“都是蓝球” |
| D、“至少有一个白球”与“都是白球” |
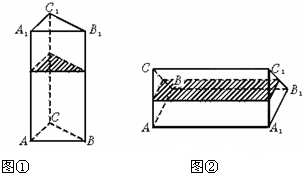 如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?
如图①是一个正三棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面.请问图①中容器内水面的高度是多少?