Question

已知⊙C：x²＋y²＋2x－4y＋1＝0.

(1)若⊙C的切线在x轴、y轴上截距相等，求切线的方程．

(2)从圆外一点P(x₀，y₀)向圆引切线PM，M为切点，O为原点，若|PM|＝|PO|，求使|PM|最小的P点坐标．

 

Answer 1

【答案】

（1）切线方程为：y＝0，y＝x，x＋y＝1＋2和x＋y＝1－2.（2）

【解析】

试题分析：⊙C：(x＋1)²＋(y－2)²＝4，圆心C(－1,2)，半径r＝2.

(1)若切线过原点设为y＝kx，则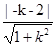＝2，∴k＝0或.

若切线不过原点，设为x＋y＝a，则＝2，∴a＝1±2，

∴切线方程为：y＝0，y＝x，x＋y＝1＋2和x＋y＝1－2.·     ·      7分

(2) 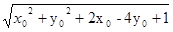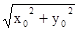＝∴2x₀－4y₀＋1＝0，      

|PM|＝＝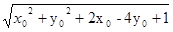

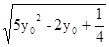
∵P在⊙C外，∴(x₀＋1)²＋(y₀－2)²>4，将x₀＝2y₀－代入得5y²－2y₀＋>0，

∴|PM|min＝.此时P.       14分

考点：圆的切线方程

点评：解决的关键是利用直线与圆的位置关系，根据点到直线的距离公式，以及两点的距离公式得到，属于基础题。