题目内容
已知⊙C:x2+y2-2x+4y-4=0,问是否存在斜率为1的直线l,使l被⊙C截得弦AB,以AB为直径的圆经过原点.若存在,写出直线l的方程;若不存在![]() ,说明理由.
,说明理由.
方法一:假设存在这样的直线l,且设为y=x+m.
⊙C化为(x-1)2+(y+2)2=9,圆心C(1,-2),则AB中点N是直线x-y+m=0与y+2=-(x![]() -1)的交点,即N(-
-1)的交点,即N(-![]() ,
,![]() ),
),
因为以AB为直径的圆过原点,所以|AN|=|ON|.
又CN⊥AB,|CN|=![]() .
.
所以|AN|=![]() =
=![]() .
.
又|ON|=![]() ,
,
由|AN|=|ON|得m=1或m=-4.
所以存在符合条件的直线l,方程为x-y+1=0或x-y-4=0.
方法二:设这样的直线存在,其方程为y=x+b,它与圆C的交点设为A(x1,y1),B(x2,y2),
则由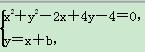
得2x2+2(b+1)x+b2+4b-4=0,
所以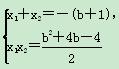 ,
,
所以y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2.
由OA⊥OB得x1x2+y1y2=0,
所以2x1x2+b(x1+x2)+b2=0,
即b2+4b-4-b(b+1)+b2=0,整理得b2+3b-4=0,
所以b=1![]() 或b=-4.
或b=-4.
所以存在符合条件的直线l,方程为x-y+1=0或x-y-4=0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =a,
=a, =b(a>2,b>2).
=b(a>2,b>2).