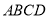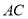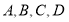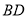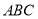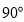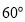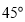题目内容
已知:以点C(t, )(t∈R,t≠0)为圆心的圆与
)(t∈R,t≠0)为圆心的圆与 轴交于点O,A,与y轴交于点O,B,其中O为原点
轴交于点O,A,与y轴交于点O,B,其中O为原点
(1)求证:△OAB的面积为定值;
(2)设直线y=–2x+4与圆C交于点M,N,若OM=ON,求圆C的方程
(1)参考解析;(2) 
【解析】
试题分析:(1)因为要证△OAB的面积为定值,关键是要求出A,B两点的坐标 根据圆的半径是 即
即 所以可以写出圆C的方程 从而分别令
所以可以写出圆C的方程 从而分别令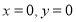 即可求得A,B两点的坐标 再根据
即可求得A,B两点的坐标 再根据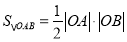 就即可证得结论
就即可证得结论
(2)因为直线y=–2x+4与圆C交于点M,N,若OM=ON 又因为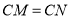 所以可得
所以可得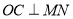 由直线
由直线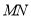 的斜率即可求得直线
的斜率即可求得直线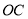 的斜率,从而得到直线
的斜率,从而得到直线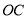 的方程,在代入C (t,
的方程,在代入C (t,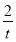 ) 即可求得
) 即可求得 的值,再根据
的值,再根据 的值判断直线与圆的关系 从而确定圆的方程
的值判断直线与圆的关系 从而确定圆的方程
试题解析:(1)因为圆C过原点O,
设圆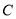 的方程是
的方程是 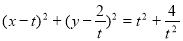 令
令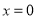 得
得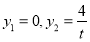 ;令
;令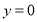 得
得 所以
所以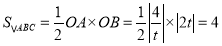 ,即
,即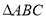 的面积为定值
的面积为定值
(2)因为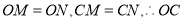 垂直平分线段
垂直平分线段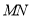 因为
因为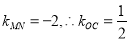 ,所以直线
,所以直线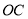 的方程是
的方程是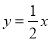 所以
所以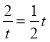 ,解得
,解得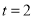 或
或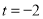 当
当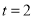 时,圆心
时,圆心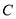 的坐标为
的坐标为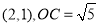
此时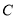 到直线
到直线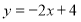 的距离
的距离 ,
,
圆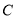 与直线
与直线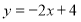 相交于两点 10分
相交于两点 10分
当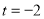 时,圆心
时,圆心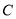 的坐标为
的坐标为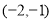 ,
,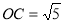 ,
,
此时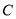 到直线
到直线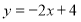 的距离
的距离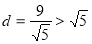
圆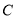 与直线
与直线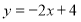 不相交,
不相交,
 不符合题意舍去 11分
不符合题意舍去 11分
 圆
圆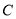 的方程为
的方程为 13分
13分
考点:1 圆的方程 2 直线与圆的方程 3 圆的对称性

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目