题目内容
已知两直线l1：ax－by＋4＝0，l2：(a－1)x＋y＋b＝0.求分别满足下列条件的a，b的值．
(1)直线l1过点(－3，－1)，并且直线l1与l2垂直；
(2)直线l1与直线l2平行，并且坐标原点到l1，l2的距离相等．
解：(1)∵l1⊥l2，
∴a(a－1)＋(－b)×1＝0，即a2－a
－b＝0.①
又点(－3，－1)在l1上，
∴－3a＋b＋4＝0.②
由①②联立得
.
(2)∵l1∥l2，∴
＝1－a，∴b＝
，
故l1和l2的方程可分别表示为：
(a－1)x＋y＋
＝0，(a－1)x＋y＋＝0，
又原点到l1与l2的距离相等．
∴4||＝||，∴a＝2或a＝
，
∴a＝2，b＝－2或a＝，b＝2.
练习册系列答案
相关题目
为了解儿子身高与其父亲身高的关
系，随机抽取5对父子的身高数据如下：
| 父亲身高x(cm) | 174 | 176 | 176 | 176 | 178 |
| 儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
则y对x的线性回归方程为( )
A．y＝x－1 B．y＝x＋1
C．y＝88＋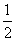
x D．y＝176
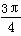，直线l1经过点A(3,2)、B(a，－1)，且l1与l垂直，直线l2：2x
＋by＋1＝0与直线l1平行，则a＋
＝－
，求直线l的方程；
时，求直线l的方程．
1