题目内容
已知常数a≠0,数列{an}的前n项和为Sn,a1=1,且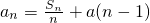 .
.
(1)求证:数列{an}为等差数列;
(2)若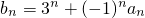 ,且数列{bn}是单调递增数列,求实数a的取值范围;
,且数列{bn}是单调递增数列,求实数a的取值范围;
(3)若 ,数列{cn}满足:
,数列{cn}满足: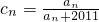 ,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
解:(Ⅰ)∵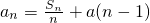
∴Sn=nan-an(n-1),an+1=Sn+1-Sn,…(2分)
∴an+1=[(n+1)an+1-a(n+1)n]-[nan-an(n-1)]
化简得:an+1-an=2a(常数),
∴数列{an}是以1为首项,公差为2a的等差数列;…(4分)
(Ⅱ)由(Ⅰ)知an=1+2a(n-1),
又∵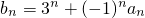 ,bn<bn+1,
,bn<bn+1,
∴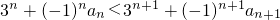 ,
,
∴(-1)n[1+(2n-1)a]<3n
①当n是奇数时,∵-[1+(2n-1)a]<3n,
∴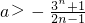 ,n=1,3,5,7,…
,n=1,3,5,7,…
令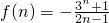 ,
,
∴a>f(n)max
∵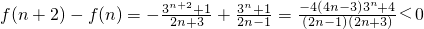
∴f(1)>f(3)>f(5)>…>f(n)>…,且f(1)=-4,
∴a>-4;…(7分)
②当n是偶数时,
∵1+(2n-1)a<3n,
∴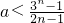 ,n=2,4,6,8,…
,n=2,4,6,8,…
令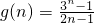 ,
,
∴a<g(n)min
∵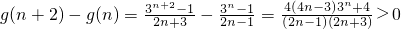
∴g(2)<g(4)<g(6)<…<g(n)<…,且 ,
,
∴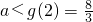 ;
;
综上可得:实数a的取值范围是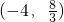 .…(10分)
.…(10分)
(Ⅲ)由(Ⅰ)知,an=n,又∵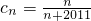 ,
,
设对任意正整数k,都存在正整数p,q,使ck=cpcq,
∴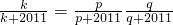 ,
,
∴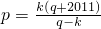 …(12分)
…(12分)
令q=k+1,则p=k(k+2012)(或q=2k,p=2k+2011)
∴ck=ck(k+2012)•ck+1(或ck=c2k+2011•c2k)…(16分)
分析:(Ⅰ)由已知利用an+1=Sn+1-Sn,代入整理化简得:an+1-an=2a(常数),可证
(Ⅱ)由(Ⅰ)知an=1+2a(n-1),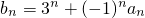 ,结合bn<bn+1,可得(-1)n[1+(2n-1)a]<3n①当n是奇数②当n是偶数,结合数列的单调性及恒成立与最值的相互转换可求a的范围
,结合bn<bn+1,可得(-1)n[1+(2n-1)a]<3n①当n是奇数②当n是偶数,结合数列的单调性及恒成立与最值的相互转换可求a的范围
(Ⅲ)由(Ⅰ)可得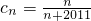 ,假设 满足ck=cpcq,代入整理可得
,假设 满足ck=cpcq,代入整理可得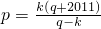 可求
可求
点评:本题综合考查了由数列的和与项的递推公式证明等差数列,及利用数列的单调性求解数列的最大(最小)项的问题及恒成立与最值求解的相互转化.
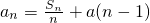
∴Sn=nan-an(n-1),an+1=Sn+1-Sn,…(2分)
∴an+1=[(n+1)an+1-a(n+1)n]-[nan-an(n-1)]
化简得:an+1-an=2a(常数),
∴数列{an}是以1为首项,公差为2a的等差数列;…(4分)
(Ⅱ)由(Ⅰ)知an=1+2a(n-1),
又∵
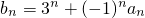 ,bn<bn+1,
,bn<bn+1,∴
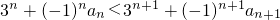 ,
,∴(-1)n[1+(2n-1)a]<3n
①当n是奇数时,∵-[1+(2n-1)a]<3n,
∴
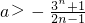 ,n=1,3,5,7,…
,n=1,3,5,7,…令
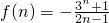 ,
,∴a>f(n)max
∵
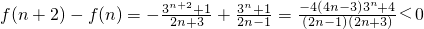
∴f(1)>f(3)>f(5)>…>f(n)>…,且f(1)=-4,
∴a>-4;…(7分)
②当n是偶数时,
∵1+(2n-1)a<3n,
∴
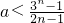 ,n=2,4,6,8,…
,n=2,4,6,8,…令
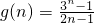 ,
,∴a<g(n)min
∵
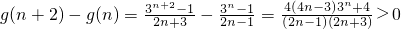
∴g(2)<g(4)<g(6)<…<g(n)<…,且
 ,
,∴
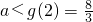 ;
;综上可得:实数a的取值范围是
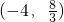 .…(10分)
.…(10分)(Ⅲ)由(Ⅰ)知,an=n,又∵
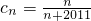 ,
,设对任意正整数k,都存在正整数p,q,使ck=cpcq,
∴
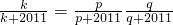 ,
,∴
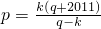 …(12分)
…(12分)令q=k+1,则p=k(k+2012)(或q=2k,p=2k+2011)
∴ck=ck(k+2012)•ck+1(或ck=c2k+2011•c2k)…(16分)
分析:(Ⅰ)由已知利用an+1=Sn+1-Sn,代入整理化简得:an+1-an=2a(常数),可证
(Ⅱ)由(Ⅰ)知an=1+2a(n-1),
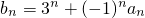 ,结合bn<bn+1,可得(-1)n[1+(2n-1)a]<3n①当n是奇数②当n是偶数,结合数列的单调性及恒成立与最值的相互转换可求a的范围
,结合bn<bn+1,可得(-1)n[1+(2n-1)a]<3n①当n是奇数②当n是偶数,结合数列的单调性及恒成立与最值的相互转换可求a的范围(Ⅲ)由(Ⅰ)可得
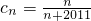 ,假设 满足ck=cpcq,代入整理可得
,假设 满足ck=cpcq,代入整理可得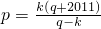 可求
可求点评:本题综合考查了由数列的和与项的递推公式证明等差数列,及利用数列的单调性求解数列的最大(最小)项的问题及恒成立与最值求解的相互转化.

练习册系列答案
相关题目
 .
. 对任意的正整数n恒成立,求实数a的取值范围;
对任意的正整数n恒成立,求实数a的取值范围; ,数列{cn}满足:
,数列{cn}满足: ,对于任意给定的正整数k,是否存在p,q∈N*,使得ck=cp•cq?若存在,求出p,q的值(只要写出一组即可);若不存在说明理由.
,对于任意给定的正整数k,是否存在p,q∈N*,使得ck=cp•cq?若存在,求出p,q的值(只要写出一组即可);若不存在说明理由.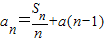 .
. ,且数列{bn}是单调递增数列,求实数a的取值范围;
,且数列{bn}是单调递增数列,求实数a的取值范围;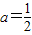 ,数列{cn}满足:
,数列{cn}满足: ,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.