��Ŀ����
��֪����a��0������{an}��ǰn���ΪSn��a1=1����an=
+a(n-1)��
��1����֤������{an}Ϊ�Ȳ����У�
��2����bn=3n+(-1)nan��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��
��3����a=
������{cn}���㣺cn=
���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ�
| Sn |
| n |
��1����֤������{an}Ϊ�Ȳ����У�
��2����bn=3n+(-1)nan��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��
��3����a=
| 1 |
| 2 |
| an |
| an+2011 |
��������������֪����an+1=Sn+1-Sn��������������ã�an+1-an=2a������������֤
�����ɣ���֪an=1+2a��n-1����bn=3n+(-1)nan�����bn��bn+1���ɵã�-1��n[1+��2n-1��a]��3n�ٵ�n�������ڵ�n��ż����������еĵ����Լ����������ֵ���ת������a�ķ�Χ
�����ɣ��ɵ�cn=
������ ����ck=cpcq�����������ɵ�p=
����
�����ɣ���֪an=1+2a��n-1����bn=3n+(-1)nan�����bn��bn+1���ɵã�-1��n[1+��2n-1��a]��3n�ٵ�n�������ڵ�n��ż����������еĵ����Լ����������ֵ���ת������a�ķ�Χ
�����ɣ��ɵ�cn=
| n |
| n+2011 |
| k(q+2011) |
| q-k |
����⣺����an=
+a(n-1)
��Sn=nan-an��n-1����an+1=Sn+1-Sn������2�֣�
��an+1=[��n+1��an+1-a��n+1��n]-[nan-an��n-1��]
����ã�an+1-an=2a����������
������{an}����1Ϊ�������Ϊ2a�ĵȲ����У�����4�֣�
�����ɣ���֪an=1+2a��n-1����
�֡�bn=3n+(-1)nan��bn��bn+1��
��3n+(-1)nan��3n+1+(-1)n+1an+1��
�ࣨ-1��n[1+��2n-1��a]��3n
�ٵ�n������ʱ����-[1+��2n-1��a]��3n��
��a��-
��n=1��3��5��7����
��f(n)=-
��
��a��f��n��max
��f(n+2)-f(n)=-
+
=
��0
��f��1����f��3����f��5��������f��n����������f��1��=-4��
��a��-4������7�֣�
�ڵ�n��ż��ʱ��
��1+��2n-1��a��3n��
��a��
��n=2��4��6��8����
��g(n)=
��
��a��g��n��min
��g(n+2)-g(n)=
-
=
��0
��g��2����g��4����g��6��������g��n����������g(2)=
��
��a��g(2)=
��
���Ͽɵã�ʵ��a��ȡֵ��Χ��(-4��
)������10�֣�
�����ɣ���֪��an=n���֡�cn=
��
�������������k��������������p��q��ʹck=cpcq��
��
=
•
��
��p=
����12�֣�
��q=k+1����p=k��k+2012������q=2k��p=2k+2011��
��ck=ck��k+2012��•ck+1����ck=c2k+2011•c2k������16�֣�
| Sn |
| n |
��Sn=nan-an��n-1����an+1=Sn+1-Sn������2�֣�
��an+1=[��n+1��an+1-a��n+1��n]-[nan-an��n-1��]
����ã�an+1-an=2a����������
������{an}����1Ϊ�������Ϊ2a�ĵȲ����У�����4�֣�
�����ɣ���֪an=1+2a��n-1����
�֡�bn=3n+(-1)nan��bn��bn+1��
��3n+(-1)nan��3n+1+(-1)n+1an+1��
�ࣨ-1��n[1+��2n-1��a]��3n
�ٵ�n������ʱ����-[1+��2n-1��a]��3n��
��a��-
| 3n+1 |
| 2n-1 |
��f(n)=-
| 3n+1 |
| 2n-1 |
��a��f��n��max
��f(n+2)-f(n)=-
| 3n+2+1 |
| 2n+3 |
| 3n+1 |
| 2n-1 |
| -4(4n-3)3n+4 |
| (2n-1)(2n+3) |
��f��1����f��3����f��5��������f��n����������f��1��=-4��
��a��-4������7�֣�
�ڵ�n��ż��ʱ��
��1+��2n-1��a��3n��
��a��
| 3n-1 |
| 2n-1 |
��g(n)=
| 3n-1 |
| 2n-1 |
��a��g��n��min
��g(n+2)-g(n)=
| 3n+2-1 |
| 2n+3 |
| 3n-1 |
| 2n-1 |
| 4(4n-3)3n+4 |
| (2n-1)(2n+3) |
��g��2����g��4����g��6��������g��n����������g(2)=
| 8 |
| 3 |
��a��g(2)=
| 8 |
| 3 |
���Ͽɵã�ʵ��a��ȡֵ��Χ��(-4��
| 8 |
| 3 |
�����ɣ���֪��an=n���֡�cn=
| n |
| n+2011 |
�������������k��������������p��q��ʹck=cpcq��
��
| k |
| k+2011 |
| p |
| p+2011 |
| q |
| q+2011 |
��p=
| k(q+2011) |
| q-k |
��q=k+1����p=k��k+2012������q=2k��p=2k+2011��
��ck=ck��k+2012��•ck+1����ck=c2k+2011•c2k������16�֣�
�����������ۺϿ����������еĺ�����ĵ��ƹ�ʽ֤���Ȳ����У����������еĵ�����������е������С��������⼰���������ֵ�����ת����

��ϰ��ϵ�д�
�����Ŀ
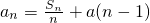 ��
��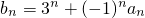 ��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��
��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ�� ������{cn}���㣺
������{cn}���㣺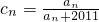 ���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ�
���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ� ��
�� �������������n���������ʵ��a��ȡֵ��Χ��
�������������n���������ʵ��a��ȡֵ��Χ�� ������{cn}���㣺
������{cn}���㣺 ���������������������k���Ƿ����p��q��N*��ʹ��ck=cp•cq�������ڣ����p��q��ֵ��ֻҪд��һ�鼴�ɣ�����������˵�����ɣ�
���������������������k���Ƿ����p��q��N*��ʹ��ck=cp•cq�������ڣ����p��q��ֵ��ֻҪд��һ�鼴�ɣ�����������˵�����ɣ�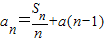 ��
�� ��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��
��������{bn}�ǵ����������У���ʵ��a��ȡֵ��Χ��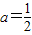 ������{cn}���㣺
������{cn}���㣺 ���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ�
���������������������k���Ƿ����p��q��N*��ʹck=cp•cq�������ڣ���p��q��ֵ��ֻҪд��һ�鼴�ɣ����������ڣ�˵�����ɣ�