题目内容
已知常数a≠0,数列{an}前n项和为Sn,且Sn=an2-(a-1)n.
(Ⅰ)求证:数列{an}为等差数列;
(Ⅱ)若an≤2n3-13n2+11n+1对任意的正整数n恒成立,求实数a的取值范围;
(Ⅲ)若a=
,数列{cn}满足:cn=
,对于任意给定的正整数k,是否存在p,q∈N*,使得ck=cp•cq?若存在,求出p,q的值(只要写出一组即可);若不存在说明理由.
(Ⅰ)求证:数列{an}为等差数列;
(Ⅱ)若an≤2n3-13n2+11n+1对任意的正整数n恒成立,求实数a的取值范围;
(Ⅲ)若a=
| 1 |
| 2 |
| an |
| an+2012 |
分析:(Ⅰ)由an=
+a(n-1),知Sn=nan-an(n-1),an+1=Sn+1-Sn,由此能够证明数列{an}是等差数列.
(Ⅱ)由an=1+2a(n-1),an≤2n3-13n2+11n+1对任意的正整数n恒成立,知1+2a(n-1)≤2n3-13n2+11n+1对任意的正整数n恒成立,故a≤
对任意的正整数n恒成立,由此能求出实数a的取值范围.
(Ⅲ)由a=
,知an=n,cn=
,因为对任意正整数k,都存在正整数p,q,使ck=cpcq,所以
=
•
,由此能够求出结果.
| Sn |
| n |
(Ⅱ)由an=1+2a(n-1),an≤2n3-13n2+11n+1对任意的正整数n恒成立,知1+2a(n-1)≤2n3-13n2+11n+1对任意的正整数n恒成立,故a≤
| 2n3-13n2+11n |
| 2(n-1) |
(Ⅲ)由a=
| 1 |
| 2 |
| n |
| n+2012 |
| k |
| k+2012 |
| p |
| p+2012 |
| q |
| q+2012 |
解答:(Ⅰ)证明:∵an=
+a(n-1),
∴Sn=nan-an(n-1),an+1=Sn+1-Sn,…(2分)
∴an+1=[(n+1)an+1-a(n+1)n]-[nan-an(n-1)]
化简得:an+1-an=2a(常数),…(4分)
∴数列{an}是以1为首项,公差为2a的等差数列;…(5分)
(Ⅱ)解:由(Ⅰ)知an=1+2a(n-1),
∵an≤2n3-13n2+11n+1对任意的正整数n恒成立,
∴1+2a(n-1)≤2n3-13n2+11n+1对任意的正整数n恒成立,…(6分)
∴a≤
对任意的正整数n恒成立,…(7分)
∴a不大于
,n∈Z+最小值.
∵
=
=n2-
n=(n-
)2-
,n∈Z+
∴当n=3时,
取最小值
-
=-20.
∴实数a的取值范围是(-∞,-20].…(10分)
(Ⅲ)解:∵an=1+2a(n-1),a=
,
∴an=n,又∵cn=
,
设对任意正整数k,都存在正整数p,q,使ck=cpcq,
∴
=
•
,
∴p=
…(14分)
令q=k+1,则p=k(k+2012)或q=2k,p=2k+2012,
∴ck=ck(k+2012)•ck+1(或)ck=c2k+2012•c2k.…(16分)
| Sn |
| n |
∴Sn=nan-an(n-1),an+1=Sn+1-Sn,…(2分)
∴an+1=[(n+1)an+1-a(n+1)n]-[nan-an(n-1)]
化简得:an+1-an=2a(常数),…(4分)
∴数列{an}是以1为首项,公差为2a的等差数列;…(5分)
(Ⅱ)解:由(Ⅰ)知an=1+2a(n-1),
∵an≤2n3-13n2+11n+1对任意的正整数n恒成立,
∴1+2a(n-1)≤2n3-13n2+11n+1对任意的正整数n恒成立,…(6分)
∴a≤
| 2n3-13n2+11n |
| 2(n-1) |
∴a不大于
| 2n3-13n2+11n |
| 2(n-1) |
∵
| 2n3-13n2+11n |
| 2(n-1) |
| n(n-1)(2n-11) |
| 2(n-1) |
| 11 |
| 2 |
| 11 |
| 4 |
| 121 |
| 16 |
∴当n=3时,
| 2n3-13n2+11n |
| 2(n-1) |
| 1 |
| 16 |
| 121 |
| 6 |
∴实数a的取值范围是(-∞,-20].…(10分)
(Ⅲ)解:∵an=1+2a(n-1),a=
| 1 |
| 2 |
∴an=n,又∵cn=
| n |
| n+2012 |
设对任意正整数k,都存在正整数p,q,使ck=cpcq,
∴
| k |
| k+2012 |
| p |
| p+2012 |
| q |
| q+2012 |
∴p=
| k(q+2012) |
| q-k |
令q=k+1,则p=k(k+2012)或q=2k,p=2k+2012,
∴ck=ck(k+2012)•ck+1(或)ck=c2k+2012•c2k.…(16分)
点评:本题考查等差数列的证明,考查实数的取值范围的求法,考查实数取值的判断.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
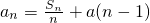 .
.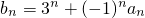 ,且数列{bn}是单调递增数列,求实数a的取值范围;
,且数列{bn}是单调递增数列,求实数a的取值范围; ,数列{cn}满足:
,数列{cn}满足: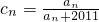 ,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由. .
. 对任意的正整数n恒成立,求实数a的取值范围;
对任意的正整数n恒成立,求实数a的取值范围; ,数列{cn}满足:
,数列{cn}满足: ,对于任意给定的正整数k,是否存在p,q∈N*,使得ck=cp•cq?若存在,求出p,q的值(只要写出一组即可);若不存在说明理由.
,对于任意给定的正整数k,是否存在p,q∈N*,使得ck=cp•cq?若存在,求出p,q的值(只要写出一组即可);若不存在说明理由.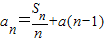 .
. ,且数列{bn}是单调递增数列,求实数a的取值范围;
,且数列{bn}是单调递增数列,求实数a的取值范围;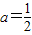 ,数列{cn}满足:
,数列{cn}满足: ,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.
,对于任意给定的正整数k,是否存在p,q∈N*,使ck=cp•cq?若存在,求p,q的值(只要写出一组即可);若不存在,说明理由.