题目内容
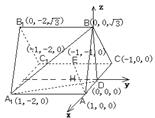
(本小题满分12分)如图,正三棱柱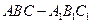 所有棱
所有棱 长都是
长都是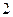 ,
,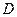 是棱
是棱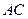 的中点,
的中点,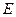 是棱
是棱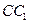 的中点,
的中点,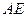 交
交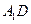 于点
于点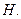
(1)求证: ;
;
(2)求二面角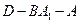 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(3)求点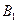 到平面
到平面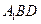 的距离.
的距离.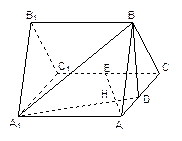
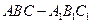 所有棱
所有棱 长都是
长都是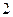 ,
,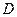 是棱
是棱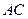 的中点,
的中点,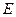 是棱
是棱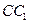 的中点,
的中点,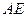 交
交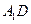 于点
于点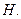
(1)求证:
 ;
;(2)求二面角
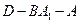 的大小(用反三角函数表示);
的大小(用反三角函数表示);(3)求点
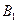 到平面
到平面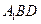 的距离.
的距离.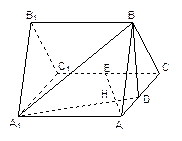
(1)略
(2)二面角D—BA1—A为锐角,它的大小为arcos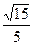
(3)B1到平面A1BD的距离d=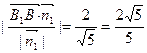
(2)二面角D—BA1—A为锐角,它的大小为arcos
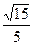
(3)B1到平面A1BD的距离d=
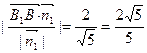
(1)证明:建立如图所示,
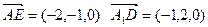
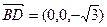
∵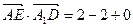
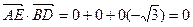

∴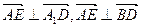 即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD
即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD
(2)设面DA1B的法向量为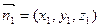
由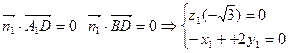 ∴取
∴取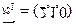
设面AA1B的法向量 为
为 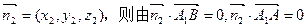
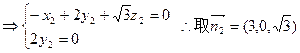 ,
, 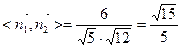
由图可知二面角D—BA1—A为锐角,∴它的大小为arcos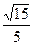
(3)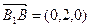 ,平面A1BD的法向量取
,平面A1BD的法向量取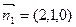
则B1到平面A1BD的距离d=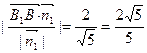
|
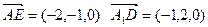
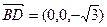
∵
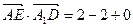
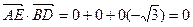

∴
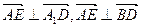 即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD
即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD(2)设面DA1B的法向量为
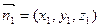
由
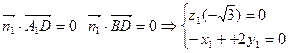 ∴取
∴取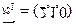
设面AA1B的法向量
 为
为 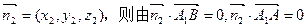
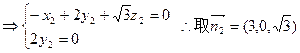 ,
, 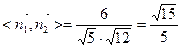
由图可知二面角D—BA1—A为锐角,∴它的大小为arcos
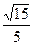
(3)
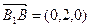 ,平面A1BD的法向量取
,平面A1BD的法向量取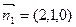
则B1到平面A1BD的距离d=
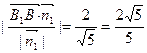

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
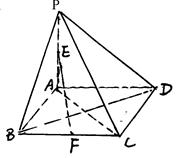
 底面ABCD,PA=AB=
底面ABCD,PA=AB=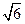 ,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。
,点E是棱PB的中点。(1)求直线AD与平面PBC的距离。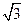 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。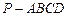 中,底面ABCD为菱形,
中,底面ABCD为菱形,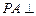 底面
底面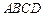 ,
,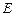 为
为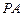 的中点,
的中点,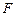 为
为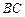 的中点,求证:
的中点,求证: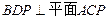 ;
; .
.
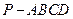 中,底面为直角梯形,
中,底面为直角梯形,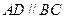 ,
,
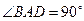 ,
,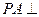 底面
底面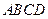 ,且
,且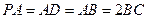 ,
,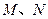 分别为
分别为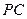 、
、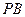 的中点。
的中点。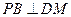 ;
;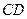 与平面
与平面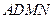 所成角的正弦值。
所成角的正弦值。
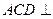 平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在
平面ABC,AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在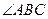 的平分线上。
的平分线上。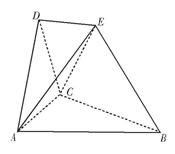
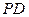 边的中点,且PA⊥底面ABCD。
边的中点,且PA⊥底面ABCD。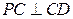

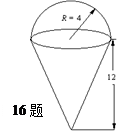
 ____.
____.
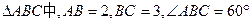 ,AD为BC边上的高,O为AD的中点,若
,AD为BC边上的高,O为AD的中点,若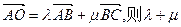 = .
= .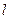 上有无数个点不在平面
上有无数个点不在平面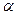 内,
内,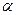
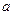 在平面
在平面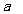 ‖
‖