题目内容
(本题满分12分)
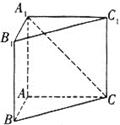
在立体图形P-ABCD中,底面ABCD是一个直角梯形,∠BAD=90°,AD∥BC,
AB=BC=a,AD=PA=2a,E是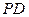 边的中点,且PA⊥底面ABCD。
边的中点,且PA⊥底面ABCD。
(1)求证:BE⊥PD
(2)求证: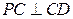
(3)求异面直线AE与CD所成的角.

在立体图形P-ABCD中,底面ABCD是一个直角梯形,∠BAD=90°,AD∥BC,
AB=BC=a,AD=PA=2a,E是
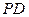 边的中点,且PA⊥底面ABCD。
边的中点,且PA⊥底面ABCD。(1)求证:BE⊥PD
(2)求证:
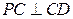
(3)求异面直线AE与CD所成的角.

(1)略
(2)略
(3)异面直线AE与CD所成的角为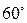
(2)略
(3)异面直线AE与CD所成的角为
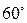
证明:(1) PA⊥底面ABCD
PA⊥底面ABCD 
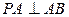
又 ∠BAD=90°
∠BAD=90° 
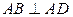

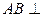 平面
平面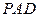
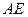 是斜线
是斜线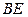 在平面
在平面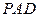 内的射影
内的射影
 AE⊥PD
AE⊥PD  BE⊥PD
BE⊥PD
(2)连结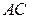
 PA⊥底面ABCD
PA⊥底面ABCD 
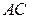 是斜线
是斜线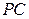 在平面
在平面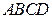 内的射影
内的射影
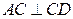

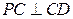
(3)过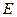 点作
点作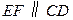 交
交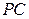 于
于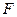 ,连结
,连结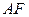 ,则
,则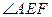 (或其补角)为异面直线AE与CD所成的角。由(2)知
(或其补角)为异面直线AE与CD所成的角。由(2)知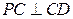
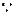
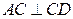

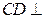 平面
平面
又
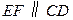

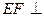 平面
平面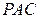

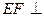
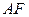
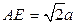
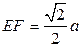
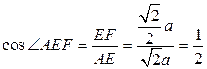

 异面直线AE与CD所成的角为
异面直线AE与CD所成的角为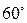
 PA⊥底面ABCD
PA⊥底面ABCD 
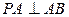
又
 ∠BAD=90°
∠BAD=90° 
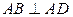

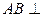 平面
平面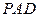
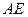 是斜线
是斜线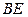 在平面
在平面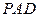 内的射影
内的射影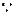 AE⊥PD
AE⊥PD  BE⊥PD
BE⊥PD(2)连结
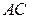
 PA⊥底面ABCD
PA⊥底面ABCD 
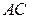 是斜线
是斜线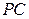 在平面
在平面 内的射影
内的射影
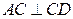

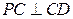
(3)过
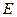 点作
点作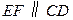 交
交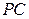 于
于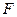 ,连结
,连结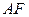 ,则
,则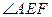 (或其补角)为异面直线AE与CD所成的角。由(2)知
(或其补角)为异面直线AE与CD所成的角。由(2)知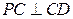
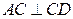

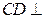 平面
平面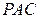
又
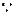
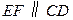

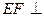 平面
平面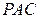

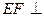
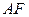
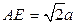
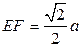
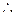
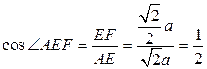
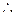

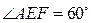
 异面直线AE与CD所成的角为
异面直线AE与CD所成的角为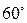

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目

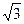 .
.
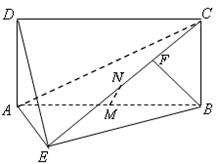
 所有棱
所有棱 长都是
长都是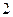 ,
,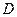 是棱
是棱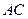 的中点,
的中点,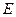 是棱
是棱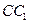 的中点,
的中点,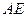 交
交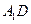 于点
于点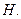
 ;
;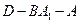 的大小(用反三角函数表示);
的大小(用反三角函数表示);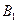 到平面
到平面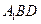 的距离.
的距离.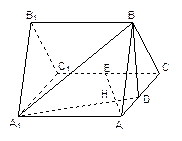
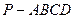 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱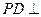 底面ABCD,
底面ABCD,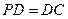 ,E是PC的中点.
,E是PC的中点.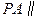 平面
平面 ;
;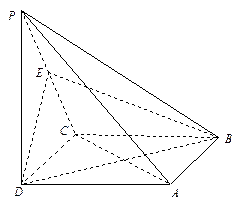
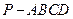 中,底面
中,底面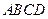 是平行四边形,
是平行四边形,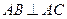 ,且
,且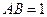 ,
,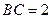 ,又
,又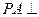 底面
底面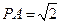 ,又
,又 为边
为边 上异于
上异于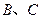 的点,且
的点,且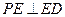 .
.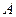 到平面
到平面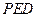 的距离.
的距离.
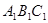 中,
中,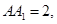 AB = 1,
AB = 1,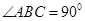 ;点D、E分别在
;点D、E分别在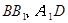 上,且
上,且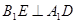 ,四棱锥
,四棱锥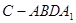 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。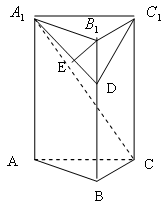
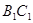 的距离;(8分)
的距离;(8分)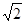 ,求二面角
,求二面角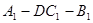 的平面角的正切值。(5分)
的平面角的正切值。(5分)
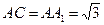 ,
,