题目内容
 将正整数按表的规律排列,把行与列交叉处的那个数称为某行某列的数,记作a(i,j)(i,j∈N*),如第2行第4列的数是15,记作a(2,4)=15,则有序数对(a(12,8),a(8,4))是
将正整数按表的规律排列,把行与列交叉处的那个数称为某行某列的数,记作a(i,j)(i,j∈N*),如第2行第4列的数是15,记作a(2,4)=15,则有序数对(a(12,8),a(8,4))是(129,53)
(129,53)
.分析:根据已知图形中数的排列的次序,归纳后分析出数的排列规律,当i为奇数时,第i列及第i行的数据将按从上到下,从右到左的顺序排列;当i为偶数时,第i列及第i行的数据将按从左到右,从下到上的顺序排列.即可找到求某行某列的数a(i,j)时的方法,由此即可得到答案.
解答:解:仔细观察图表可知,
当i为奇数时,第i列及第i行的数据将按从上到下,从右到左的顺序排列,
即:a1i,a2i,a3i,…aii,a ii-1,…ai1逐渐增大,且ai1=i×i=i2,
.当i为偶数时,第i列及第i行的数据将按从左到右,从下到上的顺序排列,
即:ai1,ai2,ai3,…aii,a i-1i,…a1i逐渐增大,且a1i=i×i=i2,
则a(11,1)=121,a(12,8)=121+8+129
a(7,1)=49,a(8,4)=49+4=53
故答案为:(129,53)
当i为奇数时,第i列及第i行的数据将按从上到下,从右到左的顺序排列,
即:a1i,a2i,a3i,…aii,a ii-1,…ai1逐渐增大,且ai1=i×i=i2,
.当i为偶数时,第i列及第i行的数据将按从左到右,从下到上的顺序排列,
即:ai1,ai2,ai3,…aii,a i-1i,…a1i逐渐增大,且a1i=i×i=i2,
则a(11,1)=121,a(12,8)=121+8+129
a(7,1)=49,a(8,4)=49+4=53
故答案为:(129,53)
点评:本题主要考查了数列的实际应用和归纳推理的解题方法,其中分析数的排列规律,由此确定关键数据的位置,是解答本题的关键,属于中档题.

练习册系列答案
相关题目
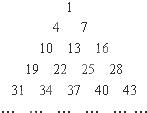 将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第4个数是( )
将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第4个数是( )| A、580 | B、577 | C、576 | D、574 |
 将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是
将正整数按一定的规则排成了如图所示的三角形数阵.根据这个排列规则,数阵中第20行从左至右的第3个数是 将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第5个数是
将正整数按一定的规则排成了如图所示的三角形数阵,根据这个排列规则,数阵中第20行从左至右的第5个数是