Question

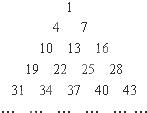将正整数按一定的规则排成了如图所示的三角形数阵．根据这个排列规则，数阵中第20行从左至右的第4个数是（　　）

• A、580
• B、577
• C、576
• D、574

Answer 1

分析：设各行的首项组成数列{a_n}，根据数列项的特点推导出第20行的第一个数，然后加9即可得到第20行从左至右的第4个数．

解答：解：解：设各行的首项组成数列{a_n}，
则a₂-a₁=3，a₃-a₂=6，…，a_n-a_n-1=3（n-1）
叠加可得：a_n-a₁=3+6+…+3（n-1）=

3n(n-1)

2

，
∴a_n=

3n(n-1)

2

+1，
∴a₂₀=

3×20×19

2

+1=571
∴数阵中第20行从左至右的第4个数是571+9=580，
故选：A．

点评：本题主要考查归纳推理的应用，利用数列项的特点，利用累加法求出每一行第一个数的规律是解决本题的关键．