题目内容
已知四面体A—BCD，AO1⊥平面BCD，且O1为ΔBCD的垂心.BO2⊥平面ACD，求证：O2是ΔACD的垂心.
解析:
证明 如图所示，连结BO1，AO2，
∵AO1⊥平面BCD，O1为ΔBCD的垂心，
∴BO1⊥CD，由三垂线定理得AB⊥CD.
又BO2⊥平面ACD，由三垂线逆定理得AO2⊥CD.
同理连结DO1，CO2可证BC⊥AD，即CO2⊥AD.
∴O2是ΔACD垂心.
练习册系列答案
相关题目
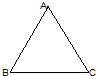已知四面体A-BCD的棱长均为2，其正视图是边长为2的等边三角形（如图，其中BC为水平线），则其侧视图的面积是（ ）A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
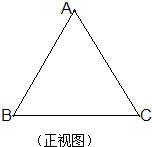已知四面体A-BCD的棱长均为2，其正视图是边长为2的等边三角形（如图，其中BC为水平线），则其侧视图的面积是
如图，已知四面体A-BCD的四个顶点都在球M的球面上，BD=2，其余棱长均为