题目内容
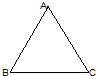 已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是( )
已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是( )A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
分析:由题意,四面体A-BCD的棱长均为2,此四面体是一个正四面体,其正视图是边长为2的等边三角形(如图,其中BC为水平线),即包含BC这一边的侧面是垂直于底面的,由此可得出其侧视图的形状,即它的度量,求出侧视图的面积,选出正确选项
解答: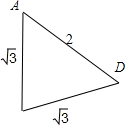 解:由题意四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),可得此四面体是一个正四面体,且包含BC这一边的侧面是垂直于底面的,故此几何体的侧视图如图
解:由题意四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),可得此四面体是一个正四面体,且包含BC这一边的侧面是垂直于底面的,故此几何体的侧视图如图
下利用海伦公式求三角形的面积
令a=
,b=
,c=2,则p=
=
+1,
由公式S=
=
=
故选A
 解:由题意四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),可得此四面体是一个正四面体,且包含BC这一边的侧面是垂直于底面的,故此几何体的侧视图如图
解:由题意四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),可得此四面体是一个正四面体,且包含BC这一边的侧面是垂直于底面的,故此几何体的侧视图如图下利用海伦公式求三角形的面积
令a=
| 3 |
| 3 |
| a+b+c |
| 2 |
| 3 |
由公式S=
| p(p-a)(p-b)(p-c) |
(
|
| 2 |
故选A
点评:本题考查由三视图求面积、体积,解答本题的关键是理解题意,得出侧视图的几何特征,是一个边长分别为
,
,2的等腰三角形,本题由于正四面体放置的位置特殊,求解时要注意领会“BC为水平线”这句话的含义.
| 3 |
| 3 |

练习册系列答案
相关题目
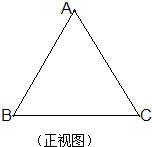 已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是
已知四面体A-BCD的棱长均为2,其正视图是边长为2的等边三角形(如图,其中BC为水平线),则其侧视图的面积是 如图,已知四面体A-BCD的四个顶点都在球M的球面上,BD=2,其余棱长均为
如图,已知四面体A-BCD的四个顶点都在球M的球面上,BD=2,其余棱长均为