题目内容
设函数f（x）=lg（1-x）-lg（1+x）．
①求它的定义域；
②判断它的奇偶性，并说明理由．
①求它的定义域；
②判断它的奇偶性，并说明理由．
考点：函数奇偶性的判断,函数的定义域及其求法
专题：计算题,函数的性质及应用
分析：①根据对数函数的定义域可知，使真数大于0即可，分别求出1-x＞0与1+x＞0，然后求出它们的交集即可；
②根据定义域是对称的，求出f（-x）与f（x）的关系，再根据奇偶性的定义进行判定即可．
②根据定义域是对称的，求出f（-x）与f（x）的关系，再根据奇偶性的定义进行判定即可．
解答：
解：①由
，得-1＜x＜1，
∴函数f（x）的定义域是{x|-1＜x＜1}；
②函数f（x）为奇函数．
理由是：
∵函数f（x）的定义域是{x|-1＜x＜1}，关于原点对称，
f（-x）=lg（1+x）-lg（1-x）=-f（x），
∴函数f（x）为奇函数．
|
∴函数f（x）的定义域是{x|-1＜x＜1}；
②函数f（x）为奇函数．
理由是：
∵函数f（x）的定义域是{x|-1＜x＜1}，关于原点对称，
f（-x）=lg（1+x）-lg（1-x）=-f（x），
∴函数f（x）为奇函数．
点评：本题主要考查了函数奇偶性的判断，以及对数函数的定义域，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知集合A={x∈R|
＜2x＜8}，B={-1，0，1，2，3}，若A∩B等于（ ）
| 1 |
| 2 |
| A、{1，2} |
| B、{-1，0，1} |
| C、{0，1，2} |
| D、{0，1，2，3} |
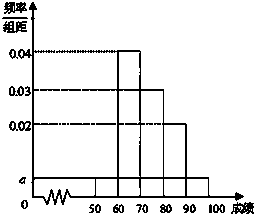某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．