��Ŀ����
����Ŀ����֪����![]() �ڵ�
�ڵ�![]() �������߷���Ϊ
�������߷���Ϊ![]() .
.
��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2������![]() �ĵ�������ͼ�ֵ.
�ĵ�������ͼ�ֵ.
���𰸡���1��![]() ;��2��������.
;��2��������.
�������������������1�����ݵ������������![]() ������
������![]() ������������
������������![]() ��
�� ![]() ��2���Ⱥ�������,���������,�б��������������ű仯����,����ȷ����������ͼ�ֵ
��2���Ⱥ�������,���������,�б��������������ű仯����,����ȷ����������ͼ�ֵ
�����������1��![]() ������Ϊ
������Ϊ![]() ����б��
�����![]() ��������
��������![]()
��![]() ��
�� ![]() �����
�����![]() ��
�� ![]()
����ʽ![]()
��2��![]()
![]()
![]() ��������Ϊ
��������Ϊ![]()
�õ�![]() ��
��![]() ��������
��������![]() ��������
��������![]() ����
����
����ֵ![]() ����Сֵ
����Сֵ![]() .
.
�����͡������
��������
20
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊ���Σ���
������![]() ��
�� ![]() ����
����![]() ��
��
![]() ��
�� ![]() ��
�� ![]() ��
��![]() �ϵ㣬��
�ϵ㣬��![]() ƽ��
ƽ��![]() .
.
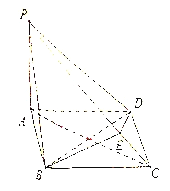
��1����֤�� ![]() ����2��������
����2��������![]() �����.
�����.
���𰸡���1��������;��2��![]() .
.
�������������������1�������������ʵöԽ������ֱ,����![]() ����
����![]() ��
��![]() ,�ٸ������洹ֱ�ж�������
,�ٸ������洹ֱ�ж�������![]() ��
��![]() ���ɵý����2����
���ɵý����2����![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ����BD Ϊ��,������POEΪ��,�����������ʽ�����
����BD Ϊ��,������POEΪ��,�����������ʽ�����
�����������1��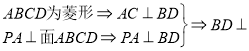 ��
��![]()
![]()
��2����![]() ��
��![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ������
������![]()
![]() ƽ��
ƽ��![]()
![]()
��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
![]() ��
�� ![]()
��![]() ��
�� ![]() ��
�� ![]() ����
����![]() ����
����![]() ��
��
��![]()
![]()
![]()

��ϰ��ϵ�д�
�����Ŀ