题目内容
3.为调查某地区老年人是否需要志愿者提供帮助,用简单的随机抽样方法从该地区调查了500名老年人,结果如下:| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(2)能够有99%的把握认为该地区老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
分析 对(1)根据列联表可求得需要志愿者提供帮助的老年人人数,再求比例;
对(2)计算K2,同临界值表进行比较,得到有多大把握认为老年人是否需要志愿者提供帮助与性别有关;
对(3)计算男、女需要提供帮助的比例,来判断分层抽样是否更切合实际.
解答 解:(1)调查的500位老人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估算值为$\frac{70}{500}$=14%.
(2)${K}^{2}=\frac{500×(40×270-30×160)^{2}}{200×300×70×430}$=9.967,由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.
(3)由(2)得结论知,该地区的老年人是否需要帮助与性别有关,并且从样本数据中能看出该地区男性老年人比女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样的方法更好.
点评 本题考查独立性检验.利用观测值K2与临界值的大小来确定是否能以一定把握认为两个分类变量有关系.
其方法是:K≥K0,解释为有[1-P(k2≥k0)]×100%的把握认为两个分类变量有关系;K<K0,解释为不能以[1-P(k2≥k0)]×100%的把握认为两个分类变量有关系.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
14.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差xi与实验室每天每100颗种子浸泡后的发芽数yi(i=1,2,…,5),作了初步处理,得到下表:
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于26”的概率;
(2)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
附:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的斜率和截距最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\sum_{i=1}^5{{x_i}{y_i}=1351}$,$\sum_{i=1}^5{x_i^2}$=615.
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差xi(0C) | 10 | 11 | 13 | 12 | 9 |
| 发芽率yi(颗) | 23 | 25 | 30 | 26 | 16 |
(2)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
附:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的斜率和截距最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\sum_{i=1}^5{{x_i}{y_i}=1351}$,$\sum_{i=1}^5{x_i^2}$=615.
11.在△ABC中,若cosA=$\frac{1}{3}$,则tanA=( )
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
 如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n根金属片从1号针移到3号针最小需要移动的次数为f(n),则f(10)1023.
如图所示:有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上:①每次只能移动一个金属片;②在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.将n根金属片从1号针移到3号针最小需要移动的次数为f(n),则f(10)1023.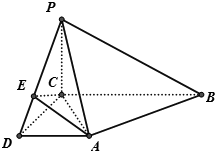 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.