题目内容
11.已知数列{an}为等差数列,a3=5,a4=2a2+a1.(1)求数列{an}的通项公式an;
(2)设bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$,数列{bn}的前n项和为Tn.
(i)求Tn;
(ii)若T1,Tm,Tn成等比数列,m>1,求正整数m,n的值.
分析 (1)设等差数列{an}的公差为d,由a3=5,a4=2a2+a1,可得$\left\{\begin{array}{l}{{a}_{1}+2d=5}\\{{a}_{1}+3d=2({a}_{1}+d)+{a}_{1}}\end{array}\right.$,解得即可得出.
(2)(i)bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,利用“裂项求和”即可得出.
(ii)由于T1,Tm,Tn成等比数列,m>1,可得${T}_{m}^{2}$=T1•Tn,化为:$\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$>0,化为2m2-4m-1<0,解出即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a3=5,a4=2a2+a1,
∴$\left\{\begin{array}{l}{{a}_{1}+2d=5}\\{{a}_{1}+3d=2({a}_{1}+d)+{a}_{1}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$,
∴an=1+2(n-1)=2n-1.
(2)(i)bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴数列{bn}的前n项和为Tn=$\frac{1}{2}[(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$.
(ii)∵T1,Tm,Tn成等比数列,m>1,
∴${T}_{m}^{2}$=T1•Tn,
∴$(\frac{m}{2m+1})^{2}$=$\frac{1}{3}×$$\frac{n}{2n+1}$,
化为:$\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$>0,
化为2m2-4m-1<0,
解得:$1-\frac{\sqrt{6}}{2}<m<1+\frac{\sqrt{6}}{2}$,
∴正整数m=2,n=12.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”方法、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.

| x(月份) | 1 | 2 | 3 | 4 | 5 | 6 |
| Q(x)(台) | 6 | 9 | 10 | 8 | 6 | 2 |
| A. | Q(x)=ax+b(a≠0) | B. | Q(x)=a|x-4|+b(a≠0) | ||
| C. | Q(x)=a(x-3)2+b(a≠0) | D. | Q(x)=a•bx(a≠0,b>0且b≠1) |
(1)根据以上数据建立一个2×2列联表,并判断在犯错误的概率不超过0.5%的前提下能否认为第一时间收看该类节目与性别有关?
(2)该研究性学习小组共有A、B、C、D和E五名同学,五人分成两组模拟“撕名牌”的游戏,其中一组三人,一组两人,求A、B两同学分在同一组的概率
参考数据:X2=$\frac{m(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
临界值表:
| P(X2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
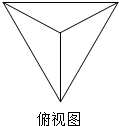
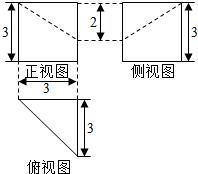
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
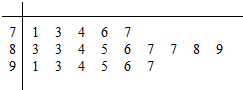 我市为了检测空气质量,每天都要记录空气质量指数(指数采用10分制,保留一位小数),现随机抽取20天的指数,绘制成如图所示的统计图(以整数部分为茎,小数部分为叶),设指数不低于8.5的视为当天空气质量为优良.
我市为了检测空气质量,每天都要记录空气质量指数(指数采用10分制,保留一位小数),现随机抽取20天的指数,绘制成如图所示的统计图(以整数部分为茎,小数部分为叶),设指数不低于8.5的视为当天空气质量为优良.