题目内容
17.若f(x)在x=x0处的导数存在,则当h→0时 $\frac{f({x}_{0}+h)-f({x}_{0}-h)}{2h}$等于( )| A. | 2 f′(x0) | B. | $\frac{1}{2}$ f′(x0) | C. | f′(x0) | D. | 4 f′(x0) |
分析 根据题意,把题目中的算式变形,再利用导数的概念即可得出答案.
解答 解:∵f(x)在x=x0处的导数存在,
∴当h→0时 $\frac{f({x}_{0}+h)-f({x}_{0}-h)}{2h}$=$\underset{lim}{h→0}$$\frac{[f{(x}_{0}+h)-f{(x}_{0})]+[f{(x}_{0})-f{(x}_{0}-h)]}{2h}$
=$\frac{1}{2}$$\underset{lim}{h→0}$$\frac{f{(x}_{0}+h)}{h}$+$\frac{1}{2}$$\underset{lim}{h→0}$$\frac{f{(x}_{0})-f{(x}_{0}-h)}{h}$
=$\frac{1}{2}$f′(x0)+$\frac{1}{2}$f′(x0)
=f′(x0).
故选:C.
点评 本题考查了导数的概念与应用问题,是基础题目.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
5.银川唐徕回民中学高中部从已编号(1~36)的36个班级中,随机抽取9个班级进行卫生大检查,用系统抽样的方法确定所选的第一组班级编号为3,则所选择第8组班级的编号是( )
| A. | 11 | B. | 27 | C. | 31 | D. | 35 |
12.y=2x关于直线y=x对称的函数为( )
| A. | $y={log_{\frac{1}{2}}}x$ | B. | $y={({\frac{1}{2}})^x}$ | C. | y=log2x | D. | y=2-x |
2.在△ABC 中,角 A,B,C 的对边分别是a,b,c,若b2=a2-c2+bc,则角 A 的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
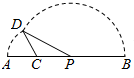 如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )
如图,线段AB=16,点C在线段AB上,且AC=6,P为段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.则△CPD面积的最大值为( )