题目内容
在各棱长都等于1的正四面体O-ABC中，若点P满足| OP |
| OA |
| OB |
| OC |
| OP |
分析：根据题中的向量等式及x+y+z=1，证出
=y
+z
，从而可得点P是平面ABC内的一点．再由正四面体O-ABC是各棱长都等于1，得到|
|的最小值等于正四面体在△ABC上的高，从而可得|
|的最小值．
| AP |
| AB |
| AC |
| OP |
| OP |
解答：解：根据题意，可得
∵点P满足
=x
+y
+z
(x+y+z=1)，
∴
=
-
=-y(
-
)-z(
-
)，
可得
=-y
-z
=y
+z
，
∴点P是平面ABC内的一点．
又∵正四面体O-ABC是各棱长都等于1，
∴当点P与O在ABC上的射影重合时，
等于正四面体的高，
此时|
|=
且
达到最小值．
故答案为：
∵点P满足
| OP |
| OA |
| OB |
| OC |
∴
| AP |
| OP |
| OA |
| OA |
| OB |
| OA |
| OC |
可得
| AP |
| BA |
| CA |
| AB |
| AC |
∴点P是平面ABC内的一点．
又∵正四面体O-ABC是各棱长都等于1，
∴当点P与O在ABC上的射影重合时，
| |OP| |
此时|
| OP |
| ||
| 3 |
| |OP| |
故答案为：
| ||
| 3 |
点评：本题给出正四面体内的点P满足的向量等式，求|
|的最小值．着重考查了空间向量的线性运算、正四面体的性质等知识，属于中档题．
| OP |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
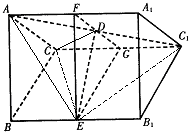如图，在正三棱柱ABC-A1B1C1中，各棱长都等于a，D、E分别是AC1、BB1的中点，
如图，正三棱柱ABC-A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1．
如图，正三棱柱ABC-A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1．
的值；