题目内容
(本小题满分10分)
已知抛物线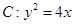 与直线
与直线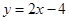 交于
交于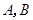 两点.
两点.
(Ⅰ)求弦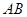 的长度;
的长度;
(Ⅱ)若点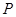 在抛物线
在抛物线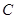 上,且
上,且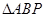 的面积为
的面积为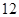 ,求点P的坐标.
,求点P的坐标.
已知抛物线
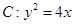 与直线
与直线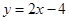 交于
交于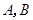 两点.
两点.(Ⅰ)求弦
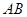 的长度;
的长度;(Ⅱ)若点
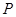 在抛物线
在抛物线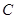 上,且
上,且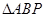 的面积为
的面积为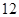 ,求点P的坐标.
,求点P的坐标.(Ⅰ)  (Ⅱ) (9,6)或(4,-4)
(Ⅱ) (9,6)或(4,-4)
 (Ⅱ) (9,6)或(4,-4)
(Ⅱ) (9,6)或(4,-4)试题分析:(Ⅰ)设A(x1,y1)、B(x2,y2),
由
 得x2-5x+4=0,Δ>0.
得x2-5x+4=0,Δ>0. 法一:又由韦达定理有x1+x2=5,x1x2=
 ,
,∴|AB|=
 =
=
法二:解方程得:x=1或4,∴A、B两点的坐标为(1,-2)、(4,4)
∴|AB|=

(Ⅱ)设点
 ,设点P到AB的距离为d,则
,设点P到AB的距离为d,则 ,∴S△PAB=
,∴S△PAB= ·
· ·
· =12,
=12,∴
 . ∴
. ∴ ,解得
,解得 或
或
∴P点为(9,6)或(4,-4).
点评:直线与圆锥曲线相交,联立方程利用韦达定理是常用的思路

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是曲线
是曲线 上的一个动点,且点
上的一个动点,且点 的中点,则动点
的中点,则动点 的轨迹方程为_____________。
的轨迹方程为_____________。 到定点
到定点 的距离比它到
的距离比它到 轴的距离大
轴的距离大 。
。 的轨迹
的轨迹 的方程;
的方程; 的直线
的直线 与
与 两点,若
两点,若 ,求弦
,求弦 的长。
的长。 上的点P到抛物线的准线的距离为
上的点P到抛物线的准线的距离为 ,到直线
,到直线 的距离为
的距离为 ,则
,则
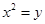 的准线方程是( )
的准线方程是( ) 经过抛物线
经过抛物线 的焦点,则实数
的焦点,则实数 =
= 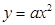 的准线方程是y=1,则此抛物线的标准方程为
的准线方程是y=1,则此抛物线的标准方程为 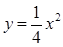 的焦点坐标是( )
的焦点坐标是( )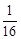 )
)