题目内容
平面内动点 到定点
到定点 的距离比它到
的距离比它到 轴的距离大
轴的距离大 。
。
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过 的直线
的直线 与
与 相交于
相交于 两点,若
两点,若 ,求弦
,求弦 的长。
的长。
 到定点
到定点 的距离比它到
的距离比它到 轴的距离大
轴的距离大 。
。(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)过
 的直线
的直线 与
与 相交于
相交于 两点,若
两点,若 ,求弦
,求弦 的长。
的长。(1) (2)8
(2)8
 (2)8
(2)8试题分析:(1)由题意,动点
 到定点
到定点 的距等于它到x=-1的距离,由抛物线的定义知,p=2,所以所求的轨迹方程为
的距等于它到x=-1的距离,由抛物线的定义知,p=2,所以所求的轨迹方程为
(2)直线
 与
与 联立,消去
联立,消去 ,整理可得:
,整理可得:
设
 ,则
,则
点评:解这道有关焦半径、焦点弦问题时,①借用到抛物线焦点弦的一个重要结论:
 ,②从整体上把握题设和目标的联系,这样可避开求解单个元素的麻烦.
,②从整体上把握题设和目标的联系,这样可避开求解单个元素的麻烦.
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 轴上,抛物线上的点
轴上,抛物线上的点 到焦点的距离为4,则
到焦点的距离为4,则 的值为( )
的值为( ) 中,设动点
中,设动点 到定点
到定点 的距离与到定直线
的距离与到定直线 的距离相等,记
的距离相等,记 .又直线
.又直线 的一个方向向量
的一个方向向量 且过点
且过点 ,
, 两点,求
两点,求 的长.
的长.
 上一点,设P到此抛物线准线的距离是d1,到直线
上一点,设P到此抛物线准线的距离是d1,到直线 的距离是d2,则dl+d2的最小值是( )
的距离是d2,则dl+d2的最小值是( )


 的准线方程为________________.
的准线方程为________________. 的准线方程为
的准线方程为 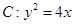 与直线
与直线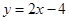 交于
交于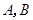 两点.
两点.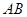 的长度;
的长度;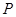 在抛物线
在抛物线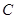 上,且
上,且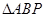 的面积为
的面积为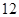 ,求点P的坐标.
,求点P的坐标. 与直线
与直线 相切,且与定圆
相切,且与定圆
 外切,求动圆圆心
外切,求动圆圆心