题目内容
已知M,N分别在△ABC的边AB和AC上,且 ,设
,设 .
.(1)若P为线段CM的中点,用
 ,
, 表示
表示 ;
;(2)设CM与BN交于点Q,求
 的值.
的值.
【答案】分析:(1)由M,N分别在△ABC的边AB和AC上,P为线段CM的中点,且 ,我们易根据向量加法的三角形法则,用
,我们易根据向量加法的三角形法则,用 ,
, 表示
表示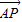 ;
;
(2)由 ,我们易将向量
,我们易将向量 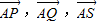 ,用
,用  ,
, 表示,利用向量加减法的运算法则,易得到
表示,利用向量加减法的运算法则,易得到  .
.
(2)由于B,Q,N三点共线,根据共线向量基本定理得:存在实数λ使得 ,同理C,Q,M三点共线,存在实数m,n使得
,同理C,Q,M三点共线,存在实数m,n使得 ,且m+n=1,综合即得结论.
,且m+n=1,综合即得结论.
解答:解:(1) ,
,
又∵ ,∴
,∴ ….(3分)
….(3分)
(2)∵ ,∴
,∴ .
.
∵B,Q,N三点共线,
∴存在实数λ使得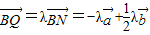 ,①
,①
∵ ,∴
,∴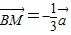 ,又
,又
∵C,Q,M三点共线,
∴存在实数m,n使得 ,且m+n=1,
,且m+n=1,
即 ,②
,②
综合①②,得 ,
,
又m+n=1,解得 ,∴
,∴ …..(10分)
…..(10分)
点评:本题考查的知识点是向量加减混合运算及其几何意义,利用向量加减法的三角形法则,及数乘向量运算法则,将平面内任一向量分解为用基底向量表示的形式,是解答本题的关键.
 ,我们易根据向量加法的三角形法则,用
,我们易根据向量加法的三角形法则,用 ,
, 表示
表示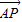 ;
;(2)由
 ,我们易将向量
,我们易将向量 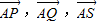 ,用
,用  ,
, 表示,利用向量加减法的运算法则,易得到
表示,利用向量加减法的运算法则,易得到  .
.(2)由于B,Q,N三点共线,根据共线向量基本定理得:存在实数λ使得
 ,同理C,Q,M三点共线,存在实数m,n使得
,同理C,Q,M三点共线,存在实数m,n使得 ,且m+n=1,综合即得结论.
,且m+n=1,综合即得结论.解答:解:(1)
 ,
,又∵
 ,∴
,∴ ….(3分)
….(3分)(2)∵
 ,∴
,∴ .
.∵B,Q,N三点共线,
∴存在实数λ使得
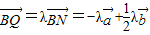 ,①
,①∵
 ,∴
,∴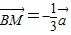 ,又
,又
∵C,Q,M三点共线,
∴存在实数m,n使得
 ,且m+n=1,
,且m+n=1,即
 ,②
,②综合①②,得
 ,
,又m+n=1,解得
 ,∴
,∴ …..(10分)
…..(10分)点评:本题考查的知识点是向量加减混合运算及其几何意义,利用向量加减法的三角形法则,及数乘向量运算法则,将平面内任一向量分解为用基底向量表示的形式,是解答本题的关键.

练习册系列答案
相关题目
 已知M,N分别在△ABC的边AB和AC上,且
已知M,N分别在△ABC的边AB和AC上,且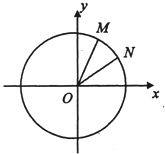 如图,在平面直角坐标系xoy中,以Ox轴为始边做两个锐角α,β,且α,β的终边依次与单位圆O相交于M、N两点,已知M、N的横坐标分别为
如图,在平面直角坐标系xoy中,以Ox轴为始边做两个锐角α,β,且α,β的终边依次与单位圆O相交于M、N两点,已知M、N的横坐标分别为