题目内容
等差数列{an}中，a1+a2+a3=3，a2+a3+a4=9，则它的公差d=（ ）
| A、-1 | B、1 | C、-2 | D、2 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由等差数列的性质和题意求出a3、a2的值，再由通项公式求出公差d．
解答：
解：由等差数列的性质得，
3a2=a1+a2+a3=3，3a3=a2+a3+a4=9，
解得a2=1，a3=3，
所以d=a3-a2=2，
故选：D．
3a2=a1+a2+a3=3，3a3=a2+a3+a4=9，
解得a2=1，a3=3，
所以d=a3-a2=2，
故选：D．
点评：本题考查了等差数列的性质、通项公式的灵活应用，难度不大．
练习册系列答案
相关题目
若函数f（x）=xn+3x在点M（1，4）处切线的斜率为3+3ln3，则n的值是（ ）
| A、3 | B、2 | C、4 | D、1 |
若a=log23，b=20.3，c=log
2，则a，b，c大小关系为（ ）
| 1 |
| 3 |
| A、a＜b＜c |
| B、a＞b＞c |
| C、a＞c＞b |
| D、b＞a＞c |
设向量
=（-1，2）
=(2，-1)，则(
•
)(
+
)等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、（1，1） |
| B、（-4，-4） |
| C、-4 |
| D、（-2，-2） |
| ∫ |
-
|
| A、0 | B、1 | C、2 | D、π |
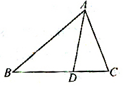在△ABC中，∠A=60°，且∠A的平分线AD将BC分成两段之比为BD：DC=2：1，又AD=