Question

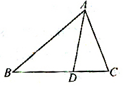在△ABC中，∠A=60°，且∠A的平分线AD将BC分成两段之比为BD：DC=2：1，又AD=4

3

．
（1）求三边长；
（2）求∠C．

Answer 1

考点：解三角形

专题：解三角形

分析：（1）利用∠A的平分线AD将BC分成两段之比为BD：DC=2：1，可得

BD

DC

=

AB

BC

=

2

1

，可设BD=2x，DC=x，AB=2y，AC=y．在△ABD与△ACD中，分别利用余弦定理解出即可．
（2）在△ABC中，利用余弦定理即可得出．

解答： 解：（1）∵∠A的平分线AD将BC分成两段之比为BD：DC=2：1，
∴

AB

BC

=

2

1

，
可设BD=2x，DC=x，AB=2y，AC=y．
在△ABD与△ACD中，分别利用余弦定理可得：
BD²=AB²+AD²-2•AB•ADcos30°，DC²=AD²+AC²-2AD•AC•cos30°．
∴4x2=4y2+(4

3

)2-2×2y×4

3

×cos30°，x2=(4

3

)2+y2-2×4

3

ycos30°．
化为x²=y²+12-6y，x²=48+y²-12y，
解得y=6，x=2

3

．
∴三边长分别为：BC=6

3

，AC=6，AB=12．
（2）在△ABC中，利用余弦定理可得：cosC=

BC2+AC2-AB2

2BC•AC

=

(6 3 )2+62-122

2×6 3 ×6

=0，
∵C∈（0°，180°）．
∴C=90°．

点评：本题考查了三角形的内角平分线的性质定理、余弦定理，考查了推理能力与计算能力，属于中档题．