题目内容
抛物线C1:y= x2(p>0)的焦点与双曲线C2:
x2(p>0)的焦点与双曲线C2:  -y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
-y2=1的右焦点的连线交C1于第一象限的点M.若C1在点M处的切线平行于C2的一条渐近线,则p等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
D解析:如图在同一坐标系中画出C1、C2草图,知C1焦点F(0,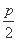 ),
),
C2右焦点F2(2,0).
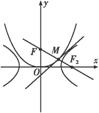
由C2渐近线方程为y=± x.
x.
直线FF2方程为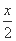 +
+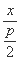 =1.联立C1与直线FF2方程得
=1.联立C1与直线FF2方程得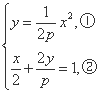
①代入②得2x2+p2x-2p2=0.
设M(x0,y0),
即2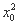 +p2x0-2p2=0.③
+p2x0-2p2=0.③
由C1得y′= x,
x,
所以 x0=
x0= ,即x0=
,即x0= p.④
p.④
由③④得p= .故选D.
.故选D.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
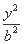 =1(b>0)的一条渐近线的方程为y=2x,则b= .
=1(b>0)的一条渐近线的方程为y=2x,则b= .  +
+ =1(a>b>0),点P(
=1(a>b>0),点P( a,
a, a)在椭圆上.
a)在椭圆上. ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+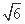 =0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.
=0相切,过点P(4,0)且不垂直于x轴直线l与椭圆C相交于A、B两点.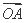 ·
·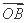 的取值范围;
的取值范围;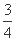 .
. ,直线l:y=kx+
,直线l:y=kx+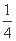 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值. -
- =1(a>0,b>0)的一条渐近线方程是y=
=1(a>0,b>0)的一条渐近线方程是y= x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )
x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为( )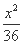 -
- 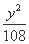 =1 (B)
=1 (B)  -
-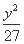 =1
=1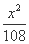 -
-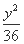 =1 (D)
=1 (D) 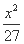 -
-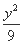 =1
=1 +y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.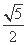 ,
, ,1),求椭圆C1的方程;
,1),求椭圆C1的方程;