题目内容
已知数列 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若 ,
, .
.
(1)求 ;
;
(2)若数列{Mn}满足条件:  ,当
,当 时,
时, -
- ,其中数列
,其中数列 单调递增,且
单调递增,且 ,
, .
.
①试找出一组 ,
, ,使得
,使得 ;
;
②证明:对于数列 ,一定存在数列
,一定存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方.
中的各数均为一个整数的平方.
(1) (2)①
(2)① ,
, ②详见解析
②详见解析
【解析】
试题分析:(1)求等差数列前n项和,一般利用待定系数法,即确定首项及公差,再代入公式即可:由 ,
, ,得
,得 解得
解得 ,所以
,所以 (2)①题目要求找出一组,因此方法为逐一代入验证,若
(2)①题目要求找出一组,因此方法为逐一代入验证,若 由
由 得
得 ,则
,则 无整数解;若
无整数解;若 由
由 得
得 ,则
,则 无整数解;若
无整数解;若 解得
解得 ②从①可归纳
②从①可归纳 ,
, ,
, ,则
,则 ,
, ,
, ,一般的取
,一般的取 ,下面只需验证
,下面只需验证 使得数列
使得数列 中的各数均为一个整数的平方.由
中的各数均为一个整数的平方.由 得
得 =
= -
- =
= ,为一整数平方.
,为一整数平方.
试题解析:(1)设数列 的首项为
的首项为 ,公差为
,公差为 ,
,
由 ,
, ,得
,得 , 2分
, 2分
解得 ,
,
所以 4分
4分
(2)①因为 ,
,
若
 ,
, ,
,
因为 ,
,
所以 ,
, ,此方程无整数解; 6分
,此方程无整数解; 6分
若
 ,
, ,
,
因为 ,
,
所以 ,
, ,此方程无整数解; 8分
,此方程无整数解; 8分
若
 ,
, ,
,
因为 ,
,
所以 ,
, ,解得
,解得 ,
,
所以 ,
, 满足题意 10分
满足题意 10分
②由①知 ,
, ,
, ,则
,则 ,
, ,
, ,
,
一般的取 , 13分
, 13分
此时 ,
, ,
,
则 =
= -
- =
= ,
,
所以 为一整数平方.
为一整数平方.
因此存在数列 ,使得数列
,使得数列 中的各数均为一个整数的平方. 16分
中的各数均为一个整数的平方. 16分
考点:等差数列与等比数列

练习册系列答案
相关题目
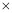 DN=____________.
DN=____________.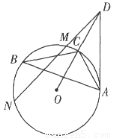
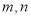 为不同的直线,
为不同的直线,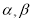 为不同的平面,则下列说法正确的是
为不同的平面,则下列说法正确的是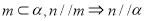
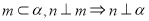
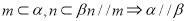
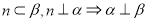
 ,则
,则 的值是 .
的值是 . ,
, ,则
,则 = .
= .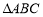 的内角
的内角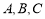 的对边分别为
的对边分别为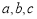 ,
,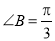 .
. 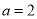 ,
,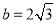 ,求
,求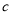 的值;
的值;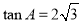 ,求
,求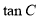 的值.
的值. ,则
,则 的值是 .
的值是 . 的直线
的直线 与圆C:
与圆C: 相切于点B,则
相切于点B,则 .
. 的前
的前 项和为
项和为 ,且
,且 ,
,  .
. ,求证:
,求证: .
.