题目内容
设向量a＝(
sinx，sinx)，b＝(cosx，sinx)，x∈
.
(1)若|a|＝|b|.求x的值；
(2)设函数f(x)＝a·b，求f(x)的最大值．
sinx，sinx)，b＝(cosx，sinx)，x∈.(1)若|a|＝|b|.求x的值；
(2)设函数f(x)＝a·b，求f(x)的最大值．
（1）x＝
（2）
（2）(1)由|a|2＝(sinx)2＋(sinx)2＝4sin2x.
|b|2＝(cosx)2＋(sinx)2＝1.
由|a|＝|b|，得4sin2x＝1，
又x∈，从而sinx＝
，所以x＝.
(2)f(x)＝a·b＝sinx·cosx＋sin2x
＝
sin2x－cos2x＋＝sin
＋，
当x＝
∈时，sin取最大值1，所以f(x)的最大值为.
sinx)2＋(sinx)2＝4sin2x.|b|2＝(cosx)2＋(sinx)2＝1.
由|a|＝|b|，得4sin2x＝1，
又x∈
，从而sinx＝，所以x＝.(2)f(x)＝a·b＝
sinx·cosx＋sin2x＝
sin2x－cos2x＋＝sin＋，当x＝
∈时，sin取最大值1，所以f(x)的最大值为.
练习册系列答案
名校课堂系列答案
相关题目
，
，
，求
的值； 
，求
的最大值。
向左平移
个单位后，得到函数
，下列关于
中心对称
轴对称
单调递增
单调递减
).
的值;
成立的x的取值集合.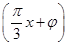
，x∈R，A>0，0<φ<
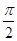，y＝f(x)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(1，A)．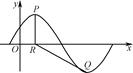
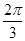，求A的值．
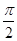)的周期为π，且图象上一个最低点为M
.
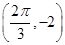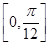时，求f(x)的最值．
，给出下列五个说法：
；②若
，则
；③
在区间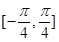
上单调递增；④函数
.⑤
成中心对称.
·cos(x＋
)的最小正周期为________．