题目内容
已知圆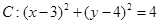 ,直线
,直线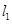 过定点A(1,0).
过定点A(1,0).
(Ⅰ)若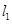 与圆相切,求
与圆相切,求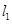 的方程;
的方程;
(Ⅱ)若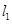 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又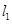 与
与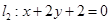 的交点为N,求证:
的交点为N,求证: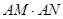 为定值.
为定值.
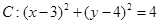 ,直线
,直线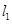 过定点A(1,0).
过定点A(1,0).(Ⅰ)若
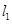 与圆相切,求
与圆相切,求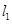 的方程;
的方程;(Ⅱ)若
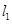 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又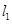 与
与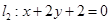 的交点为N,求证:
的交点为N,求证: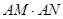 为定值.
为定值.(Ⅰ)若直线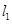 的斜率不存在,即直线是
的斜率不存在,即直线是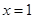 ,符合题意. -------------2分
,符合题意. -------------2分
若直线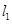 斜率存在,设直线
斜率存在,设直线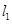 为
为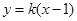 ,即
,即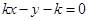 .
.
题意知,圆心(3,4)到已知直线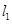 的距离等于半径2,
的距离等于半径2,
即: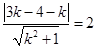 解得
解得 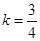 .所求直线方程是
.所求直线方程是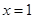 ,
,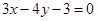 . -- 5分
. -- 5分
(Ⅱ)直线与圆相交,斜率必定存在,且不为0,可设直线方程为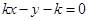
由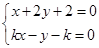 得
得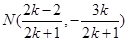 . --------------------8分
. --------------------8分
再由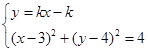 得
得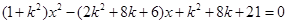 .
.
∴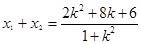 得
得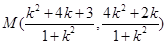 .---------- 10分
.---------- 10分
∴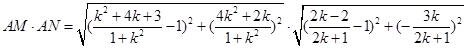
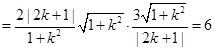 为定值.
为定值.
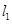 的斜率不存在,即直线是
的斜率不存在,即直线是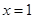 ,符合题意. -------------2分
,符合题意. -------------2分若直线
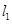 斜率存在,设直线
斜率存在,设直线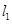 为
为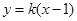 ,即
,即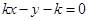 .
.题意知,圆心(3,4)到已知直线
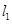 的距离等于半径2,
的距离等于半径2,即:
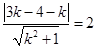 解得
解得 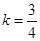 .所求直线方程是
.所求直线方程是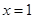 ,
,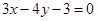 . -- 5分
. -- 5分(Ⅱ)直线与圆相交,斜率必定存在,且不为0,可设直线方程为
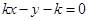
由
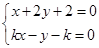 得
得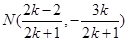 . --------------------8分
. --------------------8分再由
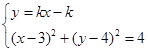 得
得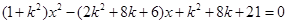 .
.∴
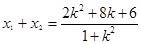 得
得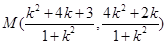 .---------- 10分
.---------- 10分∴
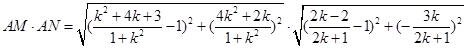
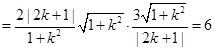 为定值.
为定值.略

练习册系列答案
相关题目
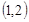 作两直线与圆
作两直线与圆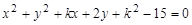 相切,则
相切,则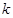 的取值范围是:( )
的取值范围是:( )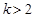
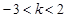
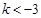 或
或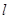 将圆:
将圆: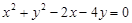 平分,且不过第四象限,则直线
平分,且不过第四象限,则直线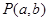 是圆
是圆 内不同于原点的一点,则直线
内不同于原点的一点,则直线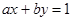 与
与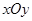 中,
中,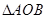 和
和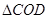 为等腰直角三角形,
为等腰直角三角形,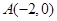 ,
,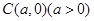 设
设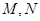 .
.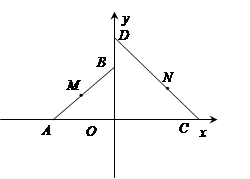
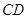 相切,求直线
相切,求直线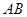 截圆N所得弦长为4,求圆N的标准方程;
截圆N所得弦长为4,求圆N的标准方程;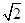 ,若存在,求此时圆N的标准方程;若不存在,说明理由.
,若存在,求此时圆N的标准方程;若不存在,说明理由.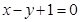 截以原点O为圆心的圆所得的弦长为
截以原点O为圆心的圆所得的弦长为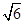
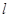 与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线
与圆O切于第一象限,且与坐标轴交于D,E,当DE长最小时,求直线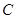 的圆心为原点,且与直线
的圆心为原点,且与直线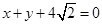 相切。
相切。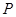 在直线
在直线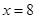 上,过
上,过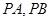 ,切点为
,切点为 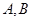 ,求证:直线
,求证:直线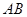 恒过定点。
恒过定点。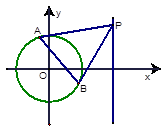
 b,且a
b,且a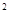 sin
sin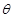 +acos
+acos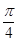 ="0" ,b
="0" ,b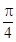 =0,则连接(a,a
=0,则连接(a,a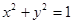 的位置关系是( )
的位置关系是( )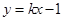 与圆
与圆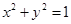 相交于P、Q两点,且
相交于P、Q两点,且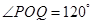 (其中Q为原点),则K的值为
(其中Q为原点),则K的值为

 ,-1
,-1