题目内容
(本小题满分16分)如图,平面直角坐标系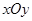 中,
中,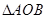 和
和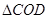 为等腰直角三角形,
为等腰直角三角形,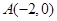 ,
,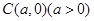 设
设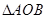 和
和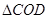 的外接圆圆心分别为
的外接圆圆心分别为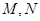 .
.
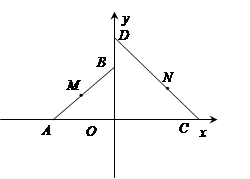
(Ⅰ)若圆M与直线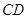 相切,求直线
相切,求直线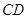 的方程;
的方程;
(Ⅱ)若直线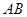 截圆N所得弦长为4,求圆N的标准方程;
截圆N所得弦长为4,求圆N的标准方程;
(Ⅲ)是否存在这样的圆N,使得圆N上有且只有三个点到直线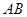 的距离为
的距离为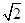 ,若存在,求此时圆N的标准方程;若不存在,说明理由.
,若存在,求此时圆N的标准方程;若不存在,说明理由.
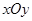 中,
中,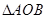 和
和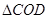 为等腰直角三角形,
为等腰直角三角形,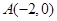 ,
,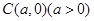 设
设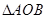 和
和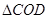 的外接圆圆心分别为
的外接圆圆心分别为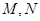 .
.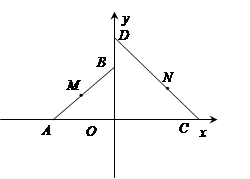
(Ⅰ)若圆M与直线
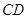 相切,求直线
相切,求直线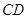 的方程;
的方程;(Ⅱ)若直线
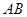 截圆N所得弦长为4,求圆N的标准方程;
截圆N所得弦长为4,求圆N的标准方程;(Ⅲ)是否存在这样的圆N,使得圆N上有且只有三个点到直线
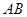 的距离为
的距离为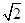 ,若存在,求此时圆N的标准方程;若不存在,说明理由.
,若存在,求此时圆N的标准方程;若不存在,说明理由.解:(1)圆心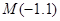 ,所以圆
,所以圆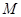 的方程为
的方程为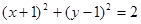 ,
,
直线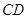 的方程为
的方程为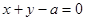 .
.
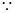 圆
圆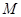 与直线
与直线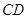 相切,
相切, 圆心
圆心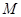 到直线
到直线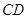 的距离
的距离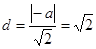 ,
,
化简得: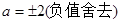 .
.
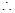 直线
直线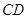 的方程为
的方程为 . ·······························5分
. ·······························5分
(2)直线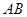 方程为:
方程为: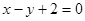 ,圆心
,圆心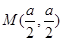 ,
,
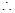 圆心
圆心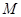 到直线
到直线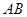 的距离为
的距离为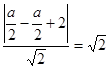 .
.
 直线
直线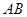 截圆
截圆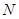 的弦长为4,
的弦长为4,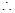
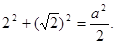
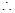
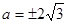 (负值舍去)
(负值舍去)
所以圆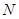 的标准方程为
的标准方程为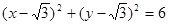 .····················10分
.····················10分
(3)存在。
由(2)知,圆心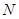 到直线
到直线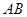 的距离为
的距离为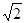 (定值),且
(定值),且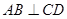 始终成立,
始终成立,
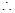 当且仅当圆
当且仅当圆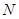 半径
半径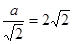 即
即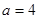 时,
时,
圆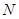 上有且只有三个点到直线
上有且只有三个点到直线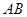 的距离为
的距离为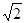 .
.
此时,圆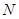 的标准方程为
的标准方程为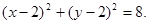 ························16分
························16分
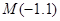 ,所以圆
,所以圆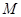 的方程为
的方程为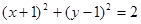 ,
,直线
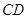 的方程为
的方程为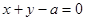 .
.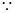 圆
圆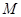 与直线
与直线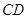 相切,
相切,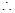 圆心
圆心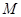 到直线
到直线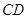 的距离
的距离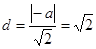 ,
,化简得:
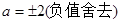 .
.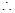 直线
直线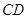 的方程为
的方程为 . ·······························5分
. ·······························5分(2)直线
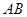 方程为:
方程为: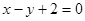 ,圆心
,圆心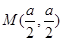 ,
,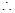 圆心
圆心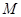 到直线
到直线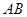 的距离为
的距离为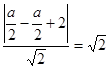 .
. 直线
直线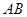 截圆
截圆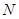 的弦长为4,
的弦长为4,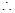
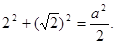
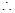
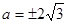 (负值舍去)
(负值舍去)所以圆
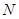 的标准方程为
的标准方程为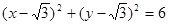 .····················10分
.····················10分(3)存在。
由(2)知,圆心
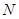 到直线
到直线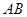 的距离为
的距离为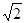 (定值),且
(定值),且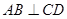 始终成立,
始终成立,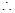 当且仅当圆
当且仅当圆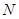 半径
半径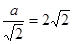 即
即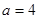 时,
时,圆
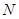 上有且只有三个点到直线
上有且只有三个点到直线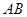 的距离为
的距离为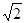 .
.此时,圆
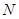 的标准方程为
的标准方程为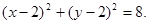 ························16分
························16分略

练习册系列答案
相关题目
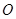 :
: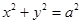 (
(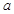 >0)
>0) 上一动点,PD
上一动点,PD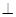
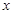 轴于D点,记线段PD的中点M的运
轴于D点,记线段PD的中点M的运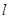 与曲线C交于A、B两点,当△OAB(O是坐标原点)面积取得最大值,且最大值为1时,求
与曲线C交于A、B两点,当△OAB(O是坐标原点)面积取得最大值,且最大值为1时,求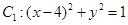 ,圆
,圆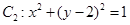 ,圆
,圆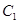 ,
,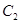 关于直线
关于直线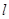 对称.
对称.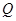 ,使
,使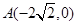 点的距离减去
点的距离减去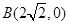 点的距离的差为
点的距离的差为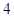 ,如果存在求出
,如果存在求出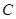 以
以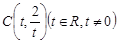 为圆心且经过原点O.
为圆心且经过原点O.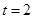 ,写出圆
,写出圆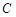 的方程;
的方程;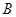 的坐标为
的坐标为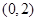 ,设
,设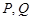 分别是直线
分别是直线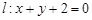 和圆
和圆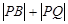 的最小值及此时点
的最小值及此时点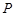 的坐标.
的坐标.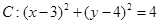 ,直线
,直线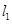 过定点A(1,0).
过定点A(1,0).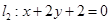 的交点为N,求证:
的交点为N,求证: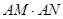 为定值.
为定值.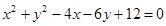 ,
,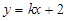 与圆C有两个不同的交点,求
与圆C有两个不同的交点,求 的取值范围.
的取值范围. 的圆心到直线
的圆心到直线 的距离为
的距离为 ,则
,则 的值为( )
的值为( ) 或
或
 或
或

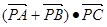 的值是 。
的值是 。