题目内容
19.已知△ABC的三个内角A,B,C的对边分别为a,b,c,设向量$\overrightarrow{m}$=(2b-c,a),$\overrightarrow{n}$=(sin2C,sinC),且满足$\overrightarrow{m}$∥$\overrightarrow{n}$,(I)求角A;
(Ⅱ)若a=3,试求b+c的取值范围.
分析 (I)由向量平行可得(2b-c)sinC=asin2C,解结合正弦定理和三角函数知识可得cosA=$\frac{1}{2}$,可得A=$\frac{π}{3}$;
(Ⅱ)可得C=$\frac{2π}{3}$-B,由正弦定理可得b+c=2$\sqrt{3}$sinB+2$\sqrt{3}$sinC,可化简为6sin(B+$\frac{π}{6}$),由0<B<$\frac{2π}{3}$和三角函数的值域可得.
解答 解:(I)∵$\overrightarrow{m}$=(2b-c,a),$\overrightarrow{n}$=(sin2C,sinC),且满足$\overrightarrow{m}$∥$\overrightarrow{n}$,
∴(2b-c)sinC=asin2C,∴(2b-c)sinC=2asinCcosC,
∴2b-c=2acosC,∴2sinB-sinC=2sinAcosC,
∴2sin(A+C)-sinC=2sinAcosC,
∴2sinAcosC+2cosAsinC-sinC=2sinAcosC,
∴2cosAsinC=sinC,即cosA=$\frac{1}{2}$,
∴角A=$\frac{π}{3}$;
(Ⅱ)∵a=3,A=$\frac{π}{3}$,∴C=$\frac{2π}{3}$-B,
由正弦定理可得$\frac{3}{\frac{\sqrt{3}}{2}}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$,
∴b+c=2$\sqrt{3}$sinB+2$\sqrt{3}$sinC=2$\sqrt{3}$sinB+2$\sqrt{3}$sin($\frac{2π}{3}$-B)
=2$\sqrt{3}$sinB+2$\sqrt{3}$($\frac{\sqrt{3}}{2}$cosB+$\frac{1}{2}$sinB)
=2$\sqrt{3}$($\frac{\sqrt{3}}{2}$cosB+$\frac{3}{2}$sinB)
=6($\frac{1}{2}$cosB+$\frac{\sqrt{3}}{2}$sinB)
=6sin(B+$\frac{π}{6}$),
∵0<B<$\frac{2π}{3}$,∴$\frac{π}{6}$<B+$\frac{π}{6}$<$\frac{5π}{6}$,
∴$\frac{1}{2}$<sin(B+$\frac{π}{6}$)≤1,
∴3<6sin(B+$\frac{π}{6}$)≤6,
∴b+c的取值范围为(3,6]
点评 本题考查解三角形,涉及向量平行和正弦定理以及三角函数的值域,属中档题.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
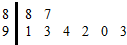 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
| A. | $f(x)=\frac{1}{x^2}$ | B. | f(x)=x2+1 | C. | f(x)=x3 | D. | f(x)=|x| |