题目内容
如图，在菱形ABCD中，∠DAB=60°，PA⊥底面ABCD，且PA=AB=2，E、F分别是AB与PD的中点.
（Ⅰ）求证：PC⊥BD；
（Ⅱ）求证：AF//平面PEC；
（Ⅲ）求二面角P―EC―D的大小；
解：（I）连结AC，则
平面ABCD，AC是斜线，PC在平面ABCD上的射影，
由三垂线定理得
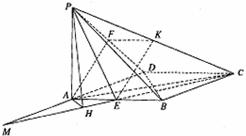
（II）取PC的中点K，连结FK、EK， 则四边形AEKF是平行四边形.
（III）延长DA、CE交于M，过A作
连结PH，由于PA⊥平面ABCD，可得
为所求二面角
的平面角.
E为AB的中点，
.
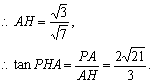
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
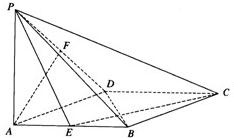如图，在菱形ABCD中，∠DAB=60°，PA⊥底面ABCD，且PA=AB=2，E、F分别是AB与PD的中点．
如图，在菱形ABCD中，MA⊥平面ABCD，且四边形ADNM是平行四边形．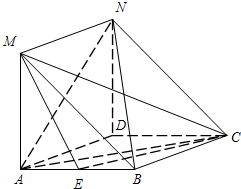
如图，在菱形ABCD中，∠DAB=60°，E是AB的中点，MA⊥平面ABCD，且在矩形ADNM中，AD=2，
（2012•大丰市一模）如图，在菱形ABCD中，E是AB的中点，且DE⊥AB．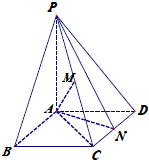
如图，在菱形ABCD中，∠BAD=120°，点N为CD中点，PA⊥平面ABCD．