题目内容
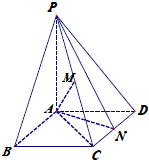 如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.
如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.(I)求证:CD⊥平面PAN;
(II)若点M为PC中点,AB=1,PA=
| 3 |
分析:(I)要证CD⊥平面PAN,可由PA⊥平面ABCD得出CD⊥PA;△ACD为正三角形,点N为CD中点,得出CD⊥AN,且PA∩AN=A而证出.
(II)过A作AH⊥PN于H,则AH⊥平面PCD,连接MH,则∠AMH为直线AM与平面PCD所成角.在RT△AMH中求解即可.
(II)过A作AH⊥PN于H,则AH⊥平面PCD,连接MH,则∠AMH为直线AM与平面PCD所成角.在RT△AMH中求解即可.
解答: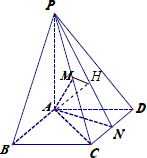 (I)证明:因为四边形ABCD为菱形,∠BAD=120°,所以△ACD为正三角形,所以AC=AD,又因为点N为CD中点,所以CD⊥AN.
(I)证明:因为四边形ABCD为菱形,∠BAD=120°,所以△ACD为正三角形,所以AC=AD,又因为点N为CD中点,所以CD⊥AN.
∵PA⊥平面ABCD,CD?平面ABCD,∴CD⊥PA.PA∩AN=A,∴CD⊥平面PAN.
(II)由(Ⅰ)知,CD⊥平面PAN,CD?平面PCD,∴平面PAN⊥平面PCD,且平面PAN∩平面PCD=PN,
过A作AH⊥PN于H,则AH⊥平面PCD,连接MH,则∠AMH为直线AM与平面PCD所成角.
在RT△PAN中,PA=
,AN=
,由勾股定理得出PN=
,根据面积相等法得AH=
=
.
在RT△PAC中,AM=
PC=
=1,
在RT△AMH中,sin∠AMH=
=
=
.即直线AM与平面PCD所成角的正弦值是
.
 (I)证明:因为四边形ABCD为菱形,∠BAD=120°,所以△ACD为正三角形,所以AC=AD,又因为点N为CD中点,所以CD⊥AN.
(I)证明:因为四边形ABCD为菱形,∠BAD=120°,所以△ACD为正三角形,所以AC=AD,又因为点N为CD中点,所以CD⊥AN.∵PA⊥平面ABCD,CD?平面ABCD,∴CD⊥PA.PA∩AN=A,∴CD⊥平面PAN.
(II)由(Ⅰ)知,CD⊥平面PAN,CD?平面PCD,∴平面PAN⊥平面PCD,且平面PAN∩平面PCD=PN,
过A作AH⊥PN于H,则AH⊥平面PCD,连接MH,则∠AMH为直线AM与平面PCD所成角.
在RT△PAN中,PA=
| 3 |
| ||
| 2 |
| ||
| 2 |
| PA•AN |
| PN |
| ||
| 5 |
在RT△PAC中,AM=
| 1 |
| 2 |
| 1 |
| 2 |
| PA2+AC2 |
在RT△AMH中,sin∠AMH=
| AH |
| AM |
| ||||
| 1 |
| ||
| 5 |
| ||
| 5 |
点评:本题考查直线和平面位置关系的判断,线面角求解.考查空间想象、推理论证、转化、计算能力.

练习册系列答案
相关题目
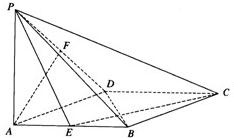 如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.
如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点. 如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.
如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.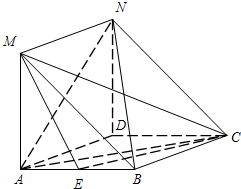 如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2,
如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2, (2012•大丰市一模)如图,在菱形ABCD中,E是AB的中点,且DE⊥AB.
(2012•大丰市一模)如图,在菱形ABCD中,E是AB的中点,且DE⊥AB.