题目内容
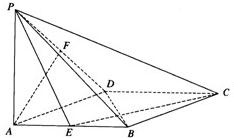 如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.
如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.(Ⅰ)求证:PC⊥BD;
(Ⅱ)求证:AF∥平面PEC;
(Ⅲ)求二面角P-EC-D的大小.
分析:(1)由于AC是斜线PC在平面ABCD上的射影,故可利用三垂线定理,转化为证明:AC⊥BD
(2)要证明AF∥平面PEC,关键是要找到平面PEC中与AF平行的直线
(3)要求二面角的大小,要先求出二面角的平面角,然后转化为解三角形问题.
(2)要证明AF∥平面PEC,关键是要找到平面PEC中与AF平行的直线
(3)要求二面角的大小,要先求出二面角的平面角,然后转化为解三角形问题.
解答: 解:(I)连接AC,则AC⊥BD.
解:(I)连接AC,则AC⊥BD.
∵PA⊥平面ABCD,AC是斜线,
PC在平面ABCD上的射影,
∴由三垂线定理得PC⊥BD.
(II)取PC的中点K,连接FK、EK,
则四边形AEKF是平行四边形,
∴AF∥EK,又EK?平面PEC,
AF?平面PEC,
∴AF∥平面PEC.
(III)延长DA、CE交于M,过A作AH⊥CM于H,
连接PH,由于PA⊥平面ABCD,可得PH⊥CM.
∴∠PHA为所求二面角P-EC-D的平面角.
∵E为AB的中点,AE∥CD,∴AM=AD=2.
在△AME中,∠MAE=120°,
由余弦定理得EM2=AM2+AE2-2AM•AEcos120°=7,
∴EM=
,又S△AEM=
AH•AE•sin120°,
∴AH=
,
∴tanPHA=
=
.
∴二面角P-EC-D的大小为arctan
 解:(I)连接AC,则AC⊥BD.
解:(I)连接AC,则AC⊥BD.∵PA⊥平面ABCD,AC是斜线,
PC在平面ABCD上的射影,
∴由三垂线定理得PC⊥BD.
(II)取PC的中点K,连接FK、EK,
则四边形AEKF是平行四边形,
∴AF∥EK,又EK?平面PEC,
AF?平面PEC,
∴AF∥平面PEC.
(III)延长DA、CE交于M,过A作AH⊥CM于H,
连接PH,由于PA⊥平面ABCD,可得PH⊥CM.
∴∠PHA为所求二面角P-EC-D的平面角.
∵E为AB的中点,AE∥CD,∴AM=AD=2.
在△AME中,∠MAE=120°,
由余弦定理得EM2=AM2+AE2-2AM•AEcos120°=7,
∴EM=
| 7 |
| 1 |
| 2 |
∴AH=
| ||
|
∴tanPHA=
| PA |
| AH |
2
| ||
| 3 |
∴二面角P-EC-D的大小为arctan
2
| ||
| 3 |
点评:线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.
判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a∥α,b?α,a∥b?a∥α);③利用面面平行的性质定理(α∥β,a?α?a∥β);④利用面面平行的性质(α∥β,a?β,a∥α?a∥β).
判断或证明线面平行的常用方法有:①利用线面平行的定义(无公共点);②利用线面平行的判定定理(a∥α,b?α,a∥b?a∥α);③利用面面平行的性质定理(α∥β,a?α?a∥β);④利用面面平行的性质(α∥β,a?β,a∥α?a∥β).

练习册系列答案
相关题目
 如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.
如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.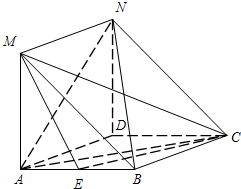 如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2,
如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2, (2012•大丰市一模)如图,在菱形ABCD中,E是AB的中点,且DE⊥AB.
(2012•大丰市一模)如图,在菱形ABCD中,E是AB的中点,且DE⊥AB.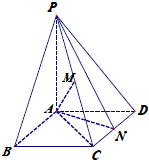 如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.
如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.