题目内容
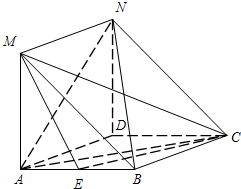 如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2,AM=
如图,在菱形ABCD中,∠DAB=60°,E是AB的中点,MA⊥平面ABCD,且在矩形ADNM中,AD=2,AM=3
| ||
| 7 |
(1)求证:AC⊥BN;
(2)求证:AN∥平面MEC;
(3)求二面角M-EC-D的大小.
分析:(1)通过连接BD,证明AC⊥平面NDB,利用BN?平面NDB,从而证明AC⊥BN;
(2)利用CM与BN交于F,连接EF.证明AN∥EF,通过直线与平面平行的判定定理证明AN∥平面MEC;
(3)通过建立空间直角坐标系,求出相关点的坐标,设平面MEC的法向量为
=(x,y,z).利用
求出向量
,求出平面ADE的法向量
,利用cosθ=
,求出二面角M-EC-D的大小.
(2)利用CM与BN交于F,连接EF.证明AN∥EF,通过直线与平面平行的判定定理证明AN∥平面MEC;
(3)通过建立空间直角坐标系,求出相关点的坐标,设平面MEC的法向量为
| n |
|
| n |
| m |
| ||||
|
|
解答: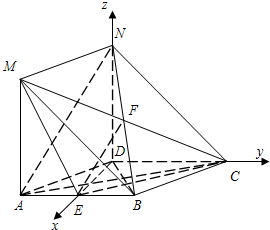 (共14分)
(共14分)
解:(1)证明:连接BD,则AC⊥BD.
由已知DN⊥平面ABCD,
因为DN∩DB=D,
所以AC⊥平面NDB.…(2分)
又因为BN?平面NDB,
所以AC⊥BN.…(4分)
(2)CM与BN交于F,连接EF.
由已知可得四边形BCNM是平行四边形,
所以F是BN的中点.
因为E是AB的中点,
所以AN∥EF.…(7分)
又EF?平面MEC,AN?平面MEC,
所以AN∥平面MEC.…(9分)
(3)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.
如图建立空间直角坐标系D-xyz,则D(0,0,0),E(
,0,0),C(0,2,0),
M(
,-1,
).
=(
,-2.0),
=(0,-1,
).…(10分)
=(0,-1,
),
设平面MEC的法向量为
=(x,y,z).
则
所以
令x=2.
所以
=(2,
,
).…(12分),
又平面ADE的法向量
=(0,0,1),
所以.cos<
,
>=
=
.
所以二面角M-EC-D的大小是60°.…(14分)
 (共14分)
(共14分)解:(1)证明:连接BD,则AC⊥BD.
由已知DN⊥平面ABCD,
因为DN∩DB=D,
所以AC⊥平面NDB.…(2分)
又因为BN?平面NDB,
所以AC⊥BN.…(4分)
(2)CM与BN交于F,连接EF.
由已知可得四边形BCNM是平行四边形,
所以F是BN的中点.
因为E是AB的中点,
所以AN∥EF.…(7分)
又EF?平面MEC,AN?平面MEC,
所以AN∥平面MEC.…(9分)
(3)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.
如图建立空间直角坐标系D-xyz,则D(0,0,0),E(
| 3 |
M(
| 3 |
3
| ||
| 7 |
| CE |
| 3 |
| EM |
3
| ||
| 7 |
| EM |
3
| ||
| 7 |
设平面MEC的法向量为
| n |
则
|
所以
|
令x=2.
所以
| n |
| 3 |
| ||
| 3 |
又平面ADE的法向量
| m |
所以.cos<
| m |
| n |
| ||||
|
|
| 1 |
| 2 |
所以二面角M-EC-D的大小是60°.…(14分)
点评:本题考查直线与平面垂直的性质,直线与平面平行的判断,二面角的求法,考查空间想象能力与计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
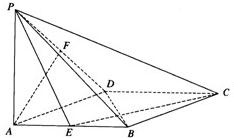 如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点.
如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,且PA=AB=2,E、F分别是AB与PD的中点. 如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.
如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形. (2012•大丰市一模)如图,在菱形ABCD中,E是AB的中点,且DE⊥AB.
(2012•大丰市一模)如图,在菱形ABCD中,E是AB的中点,且DE⊥AB.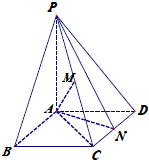 如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.
如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.