题目内容
已知抛物线y2=2x,直线l过点(0,2)与抛物线交于M,N两点,以线段MN的长为直径的圆过坐标原点O,求直线l的方程.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设直线l的方程为y=kx+2,(k≠0)M(x1,y1),N(x2,y2).与抛物线的方程联立可得k2x2+(4k-2)x+4=0,由△>0,解得k<
.由于以线段MN的长为直径的圆过坐标原点O,可得
•
=x1x2+y1y2=(1+k2)x1x2+2k(x1+x2)+4=0,把根与系数的关系代入可得k.
| 1 |
| 4 |
| OM |
| ON |
解答:
解:设直线l的方程为y=kx+2,(k≠0)M(x1,y1),N(x2,y2).
联立
,化为k2x2+(4k-2)x+4=0,
△=(4k-2)2-16k2>0,解得k<
.
∴x1+x2=
,x1x2=
.
∵以线段MN的长为直径的圆过坐标原点O,
∴
•
=x1x2+y1y2=x1x2+(kx1+2)(kx2+2)=(1+k2)x1x2+2k(x1+x2)+4=0,
∴
+
+4=0,
化为k=-1.
∴直线l的方程为y=-x+2.
联立
|
△=(4k-2)2-16k2>0,解得k<
| 1 |
| 4 |
∴x1+x2=
| 2-4k |
| k2 |
| 4 |
| k2 |
∵以线段MN的长为直径的圆过坐标原点O,
∴
| OM |
| ON |
∴
| 4(1+k2) |
| k2 |
| 2k(2-4k) |
| k2 |
化为k=-1.
∴直线l的方程为y=-x+2.
点评:本题考查了抛物线与圆的标准方程及其性质、直线与抛物线相交转化为方程联立可得△>0及其根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
如图所示,是一个空间几何体的三视图,则这个空间几何体是( )


| A、长方体 | B、球 | C、圆锥 | D、圆柱 |
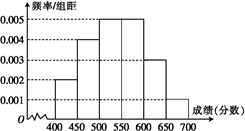 为对考生的月考成绩进行分析,某地区随机抽查了10000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.
为对考生的月考成绩进行分析,某地区随机抽查了10000名考生的成绩,根据所得数据画了如下的样本频率分布直方图.