题目内容
4．若2（x-$\frac{1}{3}$$\overrightarrow{a}$）-$\frac{1}{2}$（$\overrightarrow{a}$-3$\overrightarrow{b}$+$\overrightarrow{c}$）+$\overrightarrow{b}$=$\overrightarrow{0}$，其中$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$为已知向量，则未知向量$\overrightarrow{x}$=$\frac{7}{12}$$\overrightarrow{a}$-$\frac{5}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$．分析 根据平面向量线性运算法则计算即可．
解答 解：2（$\overrightarrow{x}$-$\frac{1}{3}$$\overrightarrow{a}$）-$\frac{1}{2}$（$\overrightarrow{a}$-3$\overrightarrow{b}$+$\overrightarrow{c}$）+$\overrightarrow{b}$=$\overrightarrow{0}$，
∴$\overrightarrow{x}$-$\frac{1}{3}$$\overrightarrow{a}$=$\frac{1}{4}$（$\overrightarrow{a}$-3$\overrightarrow{b}$+$\overrightarrow{c}$）-$\frac{1}{2}$$\overrightarrow{b}$，
∴$\overrightarrow{x}$=$\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{4}$（$\overrightarrow{a}$-3$\overrightarrow{b}$+$\overrightarrow{c}$）-$\frac{1}{2}$$\overrightarrow{b}$=（$\frac{1}{3}$+$\frac{1}{4}$）$\overrightarrow{a}$-（$\frac{3}{4}$+$\frac{1}{2}$）$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$=$\frac{7}{12}$$\overrightarrow{a}$-$\frac{5}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$．
故答案为：$\frac{7}{12}$$\overrightarrow{a}$-$\frac{5}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$．
点评 本题考查了向量的加减的运算和向量的几何意义，属于基础题．
| A． | [2，+∞） | B． | （2，+∞） | C． | [$\sqrt{3}$，+∞） | D． | （-$\sqrt{3}$，+∞） |
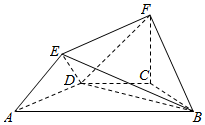如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，若CB=CD=CF=a．