题目内容

双曲线
x2
25
-
y2
16
=1的渐近线方程是（　　）
A、y=±
16
25
x
B、y=±
25
16
x
C、y=±
5
4
x
D、y=±
4
5
x
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：令双曲线的右边为0，即可得到双曲线的渐近线方程．
解答： 解：由
x2
25
-
y2
16
=0的，可得双曲线
x2
25
-
y2
16
=1的渐近线方程是y=±
4
5
x．
故选：D
点评：熟练掌握双曲线的方程与渐近线的方程的关系是解题的关键．
练习册系列答案
相关题目
已知点A（3，1），B（1，-1），则线段AB中点坐标是（　　）
A、（1，1）
B、（2，0）
C、（2，1）
D、（4，0）
某学校高一、高二、高三年级的学生人数之比为3：4：3，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则应从高二年级抽取（　　）名学生．
A、15B、20C、25D、30
不等式
3x-1
x-2
≤-1的解集是（　　）
A、{x|
3
4
≤x≤2}
B、{x|
3
4
≤x＜2}
C、{x|x＞2或x≤
3
4
}
D、{x|x＜2}
5i2014
2-i
=（　　）
A、-2+iB、-2-i
C、-1-2iD、-1+2i
由①正方形的对角线相等；②矩形的对角线相等；③正方形是矩形．写一个“三段论”形式的推理，则作为大前提、小前提和结论的分别为（　　）
A、②①③B、③①②
C、①②③D、②③①
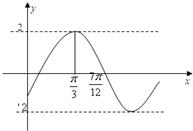已知函数y=Asin（ωx+φ）（ω＞0，A＞0，|φ|＜
π
2
）的部分图象如图所示，则f（x）的解析式为（　　）
A、y=sin（2x+
π
6
）
B、y=2sin（x-
π
6
）
C、y=2sin（2x-
π
6
）
D、y=2sin（2x+
π
6
）
若|x|≤
π
4
，则函数f（x）=cos2x+sinx的最小值是（　　）
A、
1
2
（
2
-1）
B、-
1
2
（
2
-1）
C、
1
2
（
2
+1）
D、-
1
2
（
2
+1）
已知函数f（x）=ex-ln（x+m），其中m∈R且m为常数．
（Ⅰ）试判断当m=0时函数f（x）在区间[1，+∞）上的单调性，并证明；
（Ⅱ）设函数f（x）在x=0处取得极值，求m的值，并讨论函数f（x）的单调性．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网