题目内容
13.已知A(-2,0),B(2,0),点C,D依次满足$|{\overrightarrow{AC}}$|=2,$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.求点D的轨迹.分析 求出向量的坐标,利用$|{\overrightarrow{AC}}$|=2,得轨迹方程,即可求点D的轨迹.
解答 解:设$C({x_0},{y_0}),D(x,y),\overrightarrow{AC}=({x_0}+2,{y_0}),\overrightarrow{AB}=(4,0)$.
$\overrightarrow{AD}$=$\frac{1}{2}$(x0+6,y0)=(x+2,y),∴x0=2x-2,y0=2y,
代入$|{\overrightarrow{AC}}$|=2,得x2+y2=1.
所以,点D的轨迹是以原点为圆心,1为半径的圆.
点评 本题考查向量知识的运用,考查轨迹方程,考查学生的计算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
1.已知复数$z=\frac{5}{2i-1}$(i为虚数单位),则z的共轭复数为( )
| A. | -1-2i | B. | -1+2i | C. | 2-i | D. | 2+i |
3.已知$f(x)=cos({ωx+\frac{π}{3}})$,且ω是函数y=ex-e2x的极值点,则f(x)的一条对称轴是( )
| A. | $x=-\frac{π}{3}$ | B. | $x=\frac{π}{3}$ | C. | $x=\frac{π}{6}$ | D. | $x=\frac{2π}{3}$ |
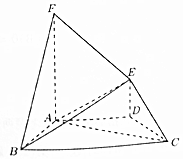 在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.
在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.