题目内容
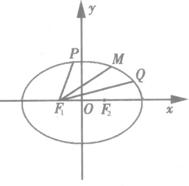
已知椭圆(1)若P、M、Q到椭圆左焦点F1的距离成等差数列,求证:线段PQ的垂直平分线经过一个定点A;
(2)若PQ为过左焦点F1且与两轴都不垂直的弦,在x轴上求一点N,使NF1为∠PNQ的平分线.
解:(1)设P(x1,y1),O(x2,y2),椭圆中a=2,b=![]() ,c=
,c=![]() ,e=
,e=![]() .
.
∵|PF1|=2+![]() x1,|MF1|=2+
x1,|MF1|=2+![]() ,|QF1|=2+
,|QF1|=2+![]() x2,依题意,2|MF1|=|PF1|+|QF1|,
x2,依题意,2|MF1|=|PF1|+|QF1|,
∴x1+x2=2,设PQ中点为C(x0,y0),
线段PQ的垂直平分线为l,则
x0=![]() ,
,
∵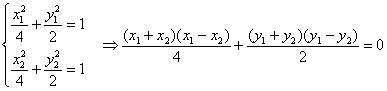
![]() +y0(y1-y2)=0
+y0(y1-y2)=0
∵y0≠0,∴kPQ=![]() ,∵PQ⊥l,∴kl=2y0,
,∵PQ⊥l,∴kl=2y0,
∴l的方程是y-y0=2y0(x-1),即
y=y0(2x-1),∴直线过定点(![]() ,0).
,0).
(2)设N(x0,0),PQ的方程为x=my-![]() 代入
代入![]() 中整理得:
中整理得:
(m2+2)y2-2![]() my-2=0,设P(x1,y1),Q(x2,y2),则
my-2=0,设P(x1,y1),Q(x2,y2),则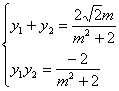
又NF1为∠PNQ的平分线,∴KNP+KNQ=0
即![]() ,
,
y1(x2-x0)+y2(x1-x0)=0,y1x2+y2x1-x0(y1+y2)=0,
y1(my2-![]() )+y2(my1-
)+y2(my1-![]() )-x0(y1+y2)=0,
)-x0(y1+y2)=0,
2m(![]() )-(x0+
)-(x0+![]() )
)![]() =0,
=0,
∴x0=-2![]() ,故N(-2
,故N(-2![]() ,0).
,0).

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目