题目内容
已知椭圆：
+
=1．
（1）若点（x，y0）为椭圆上的任意一点，求证：直线
+
=1为椭圆的切线；
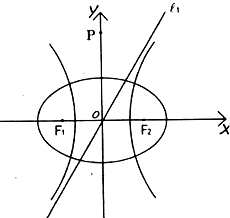
（2）若点P为直线x+y-4=0上的任意一点，过P作椭圆的切线PM、PN，其中M、N为切点，试求椭圆的右焦点F到直线MN的距离的最大值．
| x2 |
| 8 |
| y2 |
| 4 |
（1）若点（x，y0）为椭圆上的任意一点，求证：直线
| x0x |
| 8 |
| y0y |
| 4 |
（2）若点P为直线x+y-4=0上的任意一点，过P作椭圆的切线PM、PN，其中M、N为切点，试求椭圆的右焦点F到直线MN的距离的最大值．
分析：（1）由题意，知2y02=8-x02，由
，得x2-2x0x+x02=0，由△=(-2x0)2-4x02=0，知直线为椭圆的切线．
（2）设P（x0，y0），则x0=4-y0，设M（x1，y1），N（x2，y2），则PM，PN切线方程为
，且过P（x0，y0），则
，故MN所在直线方程x0x+2y0y-8=0，由此能求出求椭圆的右焦点F到直线MN的距离的最大值．
|
（2）设P（x0，y0），则x0=4-y0，设M（x1，y1），N（x2，y2），则PM，PN切线方程为
|
|
解答：解：（1）由题意，x02+2y02=8，即2y02=8-x02，…①
由
，
则（2y02+x0 2）x2-16x0x+64-16y02=0，（4分）
代入①式，得x2-2x0x+x02=0，
则△(-2x0)2-4x02=0，
∴直线为椭圆的切线（6分）
（2）设P（x0，y0），则x0+y0-4=0，即x0=4-y0，
设M（x1，y1），N（x2，y2），
则由（1）知，PM，PN切线方程为
，
且过P（x0，y0），则
，
∴MN所在直线方程为
+
=1，
即x0x+2y0y-8=0，（10分）
设所求距离为d，且F（2，0），
则d=
=
=
=
，
∴当y0=4时，dmin=1．（15分）
由
|
则（2y02+x0 2）x2-16x0x+64-16y02=0，（4分）
代入①式，得x2-2x0x+x02=0，
则△(-2x0)2-4x02=0，
∴直线为椭圆的切线（6分）
（2）设P（x0，y0），则x0+y0-4=0，即x0=4-y0，
设M（x1，y1），N（x2，y2），
则由（1）知，PM，PN切线方程为
|
且过P（x0，y0），则
|
∴MN所在直线方程为
| x0x |
| 8 |
| y0y |
| 4 |
即x0x+2y0y-8=0，（10分）
设所求距离为d，且F（2，0），
则d=
| |2x0-8| | ||
|
=
| |2y0| | ||
|
=
| 2 | ||||||
|
=
| 2 | ||||
|
∴当y0=4时，dmin=1．（15分）
点评：本题主要考查椭圆标准方程，简单几何性质，直线与椭圆的位置关系等基础知识．考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知椭圆