题目内容
已知圆的方程式x2+y2=r2，经过圆上一点M（x0，y0）的切线方程为x0x+y0y=r2，类别上述方法可以得到椭圆| x2 |
| a2 |
| y2 |
| b2 |
分析：由过圆x2+y2=r2上一点的切线方程x0x+y0y=r2，我们不难类比推断出过椭圆上一点的切线方程：用x0x代x2，用y0y代y2，即可得．
解答：解：类比过圆上一点的切线方程，可合情推理：
过椭圆
+
=1（a＞b＞0），上一点P（x0，y0）处的切线方程为
x+
y=1．
故答案为：
+
=1．
过椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x0 |
| a2 |
| y0 |
| b2 |
故答案为：
| x0x |
| a2 |
| y0y |
| b2 |
点评：本题考查椭圆的应用、利用类比推理得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论．
练习册系列答案
相关题目
类似的性质为：经过椭圆上一点M（x0，y0）的切线方程为________．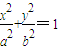
类似的性质为：经过椭圆上一点M（x，y）的切线方程为 ．