题目内容
【题目】已知a,b,c分别为![]() 内角A,B,C的对边,若
内角A,B,C的对边,若![]() 同时满足以下四个条件中的三个:①
同时满足以下四个条件中的三个:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
(1)条件①②能否同时满足,请说明理由;
(2)以上四个条件,请在满足三角形有解的所有组合中任选一组,并求出对应![]() 的面积.
的面积.
【答案】(1)不能同时满足①② (2)若![]() 满足①③④时,则
满足①③④时,则![]() 的面积为
的面积为![]() ,若
,若![]() 满足②③④时,则
满足②③④时,则![]() 的面积为
的面积为![]() .
.
【解析】
(1)由①根据余弦定理得到![]() ,进一步得到
,进一步得到![]() ,由②结合正弦定理得到
,由②结合正弦定理得到![]() ,从而得到
,从而得到![]() 不成立,由此可得答案;
不成立,由此可得答案;
(2)由(1)知,![]() 满足①③④或②③④,若
满足①③④或②③④,若![]() 满足①③④,根据余弦定理求出
满足①③④,根据余弦定理求出![]() ,再根据三角形的面积公式可得面积;若
,再根据三角形的面积公式可得面积;若![]() 满足②③④,根据正弦定理得到
满足②③④,根据正弦定理得到![]() ,由勾股定理求出
,由勾股定理求出![]() ,根据直角三角形的面积公式可得面积.
,根据直角三角形的面积公式可得面积.
(1)由①![]() 得:
得:![]()
由余弦定理![]() .
.
由②![]() 及正弦定理,得:
及正弦定理,得:
![]() ,
,
即![]() ,因为
,因为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
因为![]() 且
且![]() ,
,
所以![]() .所以
.所以![]() ,矛盾.
,矛盾.
所以![]() 不能同时满足①②.
不能同时满足①②.
(2)由(1)知,![]() 满足①③④或②③④
满足①③④或②③④
若![]() 满足①③④
满足①③④
因为![]()
所以![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 的面积
的面积![]()
另:若![]() 满足②③④
满足②③④
![]() ,即
,即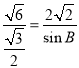 ,则
,则![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的面积
的面积![]() .
.

练习册系列答案
相关题目