题目内容
“a=1”是“函数f(x)=|x﹣a|在区间[1,+∞)上为增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
解析试题分析:当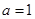 时,
时,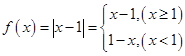 ,此时函数
,此时函数 在
在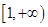 上单调递增;当函数
上单调递增;当函数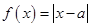 在
在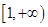 上单调递增时,则在
上单调递增时,则在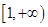 上
上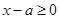 即
即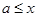 恒成立,所以
恒成立,所以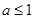 。故
。故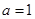 是函数
是函数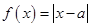 在
在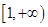 上为增函数的充分不必要条件。故A正确。
上为增函数的充分不必要条件。故A正确。
考点:1函数的单调性;2充分必要条件。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列四个命题: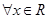 ,
,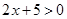 ”是全称命题;
”是全称命题;
命题“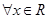 ,
,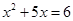 ”的否定是“
”的否定是“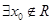 ,使
,使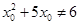 ”;
”;
若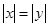 ,则
,则 ;
;
若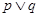 为假命题,则
为假命题,则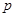 、
、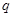 均为假命题.
均为假命题.
其中真命题的序号是( )
| A.①② | B.①④ | C.②④ | D.①②③④ |
“a=-1”是“直线a2x-y+6=0与直线4x-(a-3)y+9=0互相垂直”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列说法正确的是( )
A.“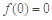 ”是“函数 ”是“函数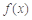 是奇函数”的充要条件 是奇函数”的充要条件 |
B.若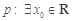 , ,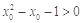 ,则 ,则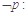 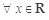 , ,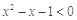 |
C.若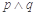 为假命题,则 为假命题,则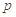 、 、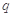 均为假命题 均为假命题 |
D.“若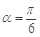 ,则 ,则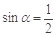 ”的否命题是“若 ”的否命题是“若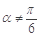 ,则 ,则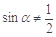 ” ” |
设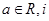 是虚数单位,则“
是虚数单位,则“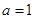 ”是“
”是“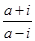 为纯虚数”的( )
为纯虚数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
已知命题p:对?x∈R,?m∈R,使4x+2xm+1=0.若命题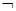 p是假命题,则实数m的取值范围是( )
p是假命题,则实数m的取值范围是( )
| A.[-2,2] | B.[2,+∞) |
| C.(-∞,-2] | D.[-2,+∞) |
已知命题p:?x∈(1,+∞),log2x<log3x;命题q:?x∈(0,+∞),2-x=lnx.则下列命题中为真命题的是( )
| A.p∧q | B.( p)∧q p)∧q |
C.p∧( q) q) | D.( p)∧( p)∧( q) q) |
“不等式x2-x+m>0在R上恒成立”的一个必要不充分条件是( )
A.m>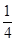 | B.0<m<1 |
| C.m>0 | D.m>1 |
下列有关命题的说法正确的是( )
A.命题“若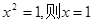 ”的否命题为:“若 ”的否命题为:“若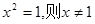 ”; ”; |
B.“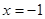 ”是“ ”是“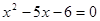 ”的必要不充分条件; ”的必要不充分条件; |
C.命题“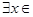 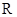 ,使得 ,使得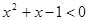 ”的否定是:“ ”的否定是:“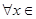 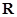 ,均有 ,均有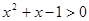 ”; ”; |
D.命题“若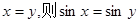 ”的逆否命题为真命题. ”的逆否命题为真命题. |