题目内容
下列说法正确的是( )
A.“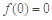 ”是“函数 ”是“函数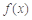 是奇函数”的充要条件 是奇函数”的充要条件 |
B.若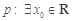 , ,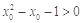 ,则 ,则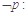 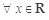 , ,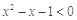 |
C.若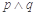 为假命题,则 为假命题,则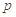 、 、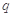 均为假命题 均为假命题 |
D.“若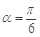 ,则 ,则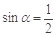 ”的否命题是“若 ”的否命题是“若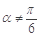 ,则 ,则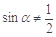 ” ” |
D
解析试题分析:A选项中,如函数 为奇函数,但
为奇函数,但 ,故不正确;
,故不正确;
B选项中,若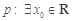 ,
,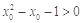 ,则
,则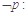
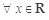 ,
, ,故B不正确;
,故B不正确;
C选项中若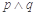 为假命题,则
为假命题,则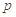 或
或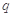 为假命题,故C不正确。故选D
为假命题,故C不正确。故选D
考点:奇函数, 命题和
命题和 命题,四种命题
命题,四种命题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“a=1”是“函数f(x)=|x﹣a|在区间[1,+∞)上为增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
给出如下四个判断:
① ;
;
② ;
;
③设 是实数,
是实数, 是
是 的充要条件 ;
的充要条件 ;
④命题“若 则
则 ”的逆否命题是若
”的逆否命题是若 ,则
,则 .
.
其中正确的判断个数是:
| A.1 | B.2 | C.3 | D.4 |
设平面向量 ,
, ,
, 均为非零向量,则“
均为非零向量,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
命题“对任意的 ”的否定是( )
”的否定是( )
A.存在 |
B.存在 |
C.不存在 |
D.对任意的 |
设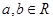 ,则“
,则“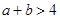 ”是“
”是“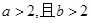 ”的( )
”的( )
| A.充分条件 | B.必要条件 |
| C.充分必要条件 | D.既非充分又非必要条件 |
[2012·浙江高考]设a∈R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分又不必要条件 |
[2013·湖南高考]“1<x<2”是“x<2”成立的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
(2011•山东)已知a,b,c∈R,命题“若a+b+c=3,则a2+b2+c2≥3”的否命题是( )
| A.若a+b+c≠3,则a2+b2+c2<3 | B.若a+b+c=3,则a2+b2+c2<3 |
| C.若a+b+c≠3,则a2+b2+c2≥3 | D.若a2+b2+c2≥3,则a+b+c=3 |