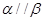题目内容
下列四个命题: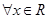 ,
,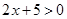 ”是全称命题;
”是全称命题;
命题“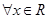 ,
,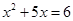 ”的否定是“
”的否定是“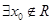 ,使
,使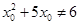 ”;
”;
若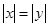 ,则
,则 ;
;
若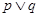 为假命题,则
为假命题,则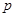 、
、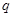 均为假命题.
均为假命题.
其中真命题的序号是( )
| A.①② | B.①④ | C.②④ | D.①②③④ |
B
解析试题分析:①因为命题中含有全称量词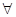 ,所以①是全称命题,所以①正确.②全称命题的否定是特称命题,所以命题“
,所以①是全称命题,所以①正确.②全称命题的否定是特称命题,所以命题“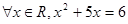 ”的否定是“
”的否定是“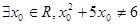 ”,所以②错误.③根据绝对值的意义可知,若
”,所以②错误.③根据绝对值的意义可知,若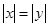 ,则
,则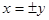 ,所以③错误.④根据复合命题的真假关系可知,若
,所以③错误.④根据复合命题的真假关系可知,若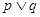 为假命题,则
为假命题,则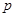 、
、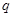 均为假命题,所以④正确.故真命题是①④.故选B.
均为假命题,所以④正确.故真命题是①④.故选B.
考点:复合命题的真假;命题的真假判断与应用.

练习册系列答案
相关题目
在 中,角
中,角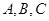 所对应的边分别为
所对应的边分别为 ,则
,则 是
是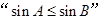 的( ).
的( ).
| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
命题“若 ”的逆否命题是( )
”的逆否命题是( )
A.若 |
B.若 |
C.若则 |
D.若 |
设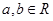 ,则“
,则“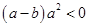 ”是“
”是“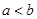 ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题 :
: ,命题
,命题 :
: 若
若 为假命题,则实数
为假命题,则实数 的取值范围为( )
的取值范围为( )
A. | B. 或 或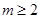 | C. | D.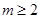 |
若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则实数a的取值范围是( )
| A.(-∞,0]∪[1,+∞) | B.(-1,0) |
| C.[-1,0] | D.(-∞,-1)∪(0,+∞) |
“a=1”是“函数f(x)=|x﹣a|在区间[1,+∞)上为增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设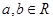 ,则“
,则“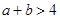 ”是“
”是“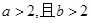 ”的( )
”的( )
| A.充分条件 | B.必要条件 |
| C.充分必要条件 | D.既非充分又非必要条件 |
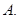 若
若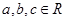 ,则
,则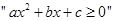 的充分条件是
的充分条件是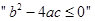
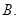 若
若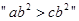 的充要条件是
的充要条件是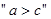
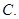 命题“对任意
命题“对任意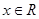 ,有
,有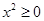 ”的否定是“存在
”的否定是“存在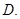
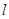 是一条直线,
是一条直线,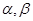 是两个不同的平面,若
是两个不同的平面,若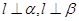 ,则
,则