题目内容
10.已知函数g(x)=logax,其中a>1.当x∈[0,1]时,g(ax+2)>1恒成立,求a的取值范围.分析 根据对数函数的图象和性质,可得当x∈[0,1]时,g(ax+2)>1恒成立,即x∈[0,1]时,ax+2>a恒成立,再由指数函数的图象和性质,可得a0+2>a,解得答案.
解答 解:∵函数g(x)=logax,其中a>1.
若当x∈[0,1]时,g(ax+2)>1恒成立,
则当x∈[0,1]时,ax+2>a恒成立,
即a0+2>a,解得:a∈(1,3).
点评 本题考查的知识点是指数函数的图象和性质,对数函数的图象和性质,难度中档.

练习册系列答案
相关题目
5.已知抛物线C的顶点在坐标原点O,焦点在x轴上,过原点的直线y=-x与抛物线C的交点为A,若P(-$\frac{1}{2}$,$\frac{1}{2}$)为OA的中点,则抛物线C的方程为y2=-x.
15.已知集合A={x|x<2},B={x|-1≤x≤3},则A∩B=( )
| A. | [-1,2) | B. | [-1,3] | C. | (-∞,3] | D. | [-1,+∞) |
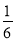 B.
B. C.
C.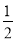 D.
D.