题目内容
在数列 中,
中, ,
, ,
, 。
。
(Ⅰ)计算 ,
, ,
, 的值;
的值;
(Ⅱ)猜想数列 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
 中,
中, ,
, ,
, 。
。(Ⅰ)计算
 ,
, ,
, 的值;
的值; (Ⅱ)猜想数列
 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明. (Ⅰ)解:由题意,得 , 3分
, 3分
(Ⅱ)解:由 ,猜想
,猜想 5分
5分
以下用数学归纳法证明:对任何的 。
。
证明:①当 时,由已知,左边
时,由已知,左边 ,右边
,右边 ,等式成立。7分
,等式成立。7分
②假设当 时,
时, 成立,
成立,
则 时,
时,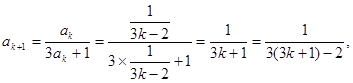
所以当 时,猜想也成立。 12分
时,猜想也成立。 12分
根据①和②,可知猜想对于任何 都成立。 13分
都成立。 13分
 , 3分
, 3分(Ⅱ)解:由
 ,猜想
,猜想 5分
5分以下用数学归纳法证明:对任何的
 。
。证明:①当
 时,由已知,左边
时,由已知,左边 ,右边
,右边 ,等式成立。7分
,等式成立。7分②假设当
 时,
时, 成立,
成立,则
 时,
时,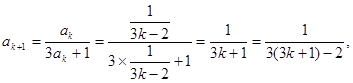
所以当
 时,猜想也成立。 12分
时,猜想也成立。 12分根据①和②,可知猜想对于任何
 都成立。 13分
都成立。 13分本试题主要是考查了数列的通项公式的求解和数学归纳法证明的运用。
(1)利用一种的递推关系可知得到前几项,然后归纳猜想其通项公式。
(2)运用数学归纳法证明的时候注意n=k和n=k+1之间的变换,以及假设的运用。
(1)利用一种的递推关系可知得到前几项,然后归纳猜想其通项公式。
(2)运用数学归纳法证明的时候注意n=k和n=k+1之间的变换,以及假设的运用。

练习册系列答案
相关题目
 的第1项
的第1项 ,且
,且 .
. ,
,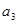 ,
, ;
; 的表达式,并用数学归纳法进行证明.
的表达式,并用数学归纳法进行证明.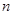 项和为
项和为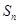 ,满足an+1=an–an–1(n≥2),
,满足an+1=an–an–1(n≥2),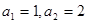 ,则
,则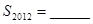
 的所有项按照从大到小,左大右小的原则写成如图所示的数表,第
的所有项按照从大到小,左大右小的原则写成如图所示的数表,第 行有
行有 个数,第
个数,第 个数(从左数起)记为
个数(从左数起)记为 ,则
,则 可记为_________.
可记为_________.
 ,
, ,
, ,
, ,…,则
,…,则 是这个数列的
是这个数列的  层台阶,若每次可上一层或两层,设上法总数为
层台阶,若每次可上一层或两层,设上法总数为 ,则下列猜想正确的是
,则下列猜想正确的是




 中,
中, ,
, ,则数列通项
,则数列通项 __________
__________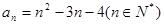 ,则a4等于( ).
,则a4等于( ).