题目内容
(本小题满分14分)
已知数列 的第1项
的第1项 ,且
,且 .
.
(1)计算 ,
,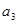 ,
, ;
;
(2)猜想 的表达式,并用数学归纳法进行证明.
的表达式,并用数学归纳法进行证明.
已知数列
 的第1项
的第1项 ,且
,且 .
.(1)计算
 ,
,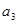 ,
, ;
;(2)猜想
 的表达式,并用数学归纳法进行证明.
的表达式,并用数学归纳法进行证明.(1)1, ,
, ,
, ;(2)
;(2) ,证明见解析.
,证明见解析.
 ,
, ,
, ;(2)
;(2) ,证明见解析.
,证明见解析.第一问中利用已知的递推关系式可知借助于首项1,得到第二项和第三项和第四项。
第二问中,根据第一问中特殊情况,推广到一般,得到猜想,然后结合数学归纳法加以证明即可。
解:(1)由题意,当n=1时, ;
;
当n=2时, ; (1分)
; (1分)
当n=3时, ; (2分)
; (2分)
当n=4时, . (3分)
. (3分)
(2)猜想 . (6分)
. (6分)
①当n=1时,猜想显然成立; (8分)
②假设当n=k( )时猜想成立,即
)时猜想成立,即 , (9分)
, (9分)
那么, , (11分)
, (11分)
所以,当n=k+1时猜想也成立. (12分)
根据①和②,可知猜想对任何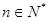 都成立. (14分)
都成立. (14分)
第二问中,根据第一问中特殊情况,推广到一般,得到猜想,然后结合数学归纳法加以证明即可。
解:(1)由题意,当n=1时,
 ;
;当n=2时,
 ; (1分)
; (1分)当n=3时,
 ; (2分)
; (2分)当n=4时,
 . (3分)
. (3分)(2)猜想
 . (6分)
. (6分)①当n=1时,猜想显然成立; (8分)
②假设当n=k(
 )时猜想成立,即
)时猜想成立,即 , (9分)
, (9分)那么,
 , (11分)
, (11分)所以,当n=k+1时猜想也成立. (12分)
根据①和②,可知猜想对任何
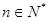 都成立. (14分)
都成立. (14分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
, ,
, 。
。 ,
, ,
, 的值;
的值;  满足:
满足: ,
, ,求数列
,求数列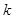 边形的内角和为
边形的内角和为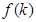 ,则
,则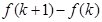 等于__________
等于__________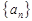 的前
的前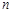 项和为
项和为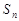 ,
,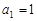 ,且
,且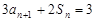 (
(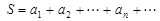 .
. 若对任意正整数
若对任意正整数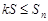 恒成立,求实数
恒成立,求实数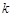 的最大值.
的最大值. 中,
中, ,
,  ,则
,则 ( )
( )



 的前
的前 项和
项和 ,则
,则 的值是( )
的值是( )



 ,
, ,………,
,………, ……的前
……的前 项和
项和 =
= 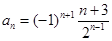 ,则
,则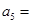 ( )
( )


