Question

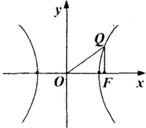已知双曲线

x2

a2

-

y2

b2

=1(a＞0，b＞0)，Q为右支上一点，F为右焦点，O为坐标原点，△OFQ的面积为2

6

，

OF

•

FQ

=m．
（1）设

6

≤m≤4

6

，求∠OFQ正切值的取值范围；
（2）若|

OF

|=c，m=(

6

4

-1)c2，求当 |

OQ

|取得最小值时，求此双曲线的方程．

Answer 1

分析：（1）利用△OFQ的面积为2

6

，

OF

•

FQ

=m，可得∠OFQ正切值，根据m的范围，即可确定∠OFQ正切值的取值范围；
（2）先确定Q的坐标，再计算 |

OQ

|的最小值，从而可求双曲线的方程．

解答：解：（1）设∠OFQ=θ，则

| OF |•| FQ |cos(π-θ)=m 1 2 •| OF |•| FQ |sinθ=2 6

，∴tanθ=-

4 6

m

∵

6

≤m≤4

6

∴-4≤tanθ≤-1
（2）设所求的双曲线方程为

x2

a2

-

y2

b2

=1(a＞0，b＞0)，Q(x1，y1)，∴

FQ

=(x1-c，y1)
∴S△OFQ=

1

2

|

OF

|•|y1|=2

6

，∴y1=±

4 6

c

又∵

OF

•

FQ

=m，∴

OF

•

FQ

=(c，0)•(x1-c，y1)=(x1-c)•c=(

6

4

-1)c2
∴x1=

6

4

c，
∴|

OQ

|=

x 2 1 + y 2 1

=

96 c2 + 3c2 8

≥

12

．
当且仅当c=4时，|

OQ

|最小，此时Q的坐标是(

6

，

6

)或(

6

，-

6

)
∴

6 a2 - 6 b2 =1 a2+b2=16

，∴

a2=4 b2=12

，
∴所求方程为

x2

4

-

y2

12

=1．

点评：当题中的条件和结论体现出一种明显的函数关系时，可通过建立目标函数，求其目标函数的最值，求函数最值的常用方法有：一元二次函数法、基本不等式法、判别式法、定义法、函数单调性法等．